
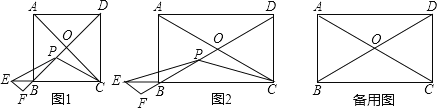
【题目】在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F
(1)如图1,当∠COD=90°时,△BEF的形状是
(2)如图2,当点P在线段BO上时,求证:OP=BF
(3)当∠COD=60°、CD=3时,请直接写出当△PEF成为直角三角形时的面积.
【答案】(1)等腰直角三角形;(2)见解析;(3)![]() .
.
【解析】
(1)根据对角线互相垂直的矩形是正方形判定矩形ABCD是正方形,再由平行线的性质和正方形的性质得∠FEB=45°,从而得:△BEF是等腰直角三角形;
(2)根据AAS证明△PEF≌△COP,可得结论;
(3)根据∠COD=60°,得△COD是等边三角形,则OC=CD=3,证明△PFE≌△COP(ASA),得PF=OC=3,根据直角三角形30度角的性质计算PE和EF的长,根据三角形的面积公式可得结论.
解:(1)△BEF是等腰直角三角形,理由是:
如图1,∵∠COD=90°,
∴AC⊥BD,
∴矩形ABCD是正方形,
∴∠ACB=45°,
∵EF∥AC,
∴∠FEB=∠ACB=45°,∠F=∠BOC=90°,
∴△BEF是等腰直角三角形,
故答案为:等腰直角三角形;
(2)如图2,∵四边形ABCD是矩形,
∴AC=BD,OB=![]() BD,OC=
BD,OC=![]() AC,
AC,
∴OB=OC,
∴∠OBC=∠OCB=∠FBE,
∵∠FBE=∠BEP+∠EPB,∠OCB=∠PCB+∠OCP,
∵PE=PC,
∴∠BEP=∠PCB,
∴∠EPB=∠OCP,
∵EF∥AC,
∴∠COP=∠BFE,
∴△PEF≌△CPO(AAS),
∴OC=PF=OB,
∴OB﹣PB=PF﹣PB,
即OP=BF;
(3)∵四边形ABCD是矩形,
∴AC=BD,OD=![]() BD,OC=
BD,OC=![]() AC,
AC,
∴OD=OC,
∵∠COD=60°,
∴△COD是等边三角形,
∴OC=CD=3,
如图3,当∠PEF=90°时,
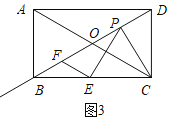
∵EF∥AC,
∴∠POC=∠OFE=60°,
∴∠BFE=120°,
∴OB=OC,
∴∠OBC=∠OCB=∠FEB=30°,
∵∠FEP=90°,
∴∠PEC=60°,
∵PE=PC,
∴△PEC是等边三角形,
∴∠PCB=60°,
∴∠PCO=60°﹣30°=30°=∠FPE,
∴△PFE≌△COP(ASA),
∴PF=OC=3,
Rt△PFE中, ![]() ,
,
![]() ;
;
∴当△PEF成为直角三角形时的面积是![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
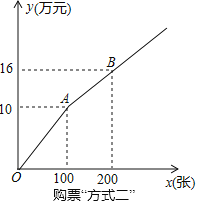
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
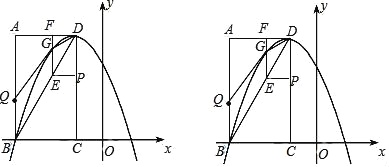
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(﹣3,4)、B(﹣3,0)、C(﹣1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.
(1)求抛物线的解析式;
(2)当t为何值时,四边形BDGQ的面积最大?最大值为多少?
(3)动点P、Q运动过程中,是否存在某一时刻,使△PQF是等腰三角形?若存在,请求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
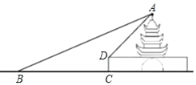
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
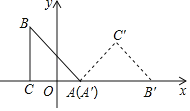
【题目】如图,等腰直角三角形ABC在平面直角坐标系中,直角边AC在x轴上,O为AC的中点,点A的坐标为(1,0),将△ABC绕点A顺时针旋转135°,使斜边AB的对应边A′B′与x轴重合,则点C的对应点C'的坐标为( )
A. (2,2)B. (1+![]() ,
,![]() )C. (1+
)C. (1+![]() ,2)D. (2
,2)D. (2![]() ,2+
,2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
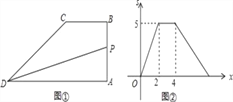
【题目】如图①,四边形ABCD中,BC∥AD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )
A. 4 B. 2+![]() C. 5 D. 4+
C. 5 D. 4+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com