
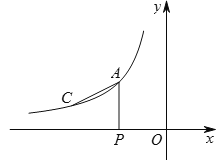
【题目】如图,点A(-2,a),C(3a-10,1)是反比例函数![]() (x<0)图象上的两点.
(x<0)图象上的两点.
(1)求m的值;
(2)过点A作AP⊥x轴于点P,若直线y=kx+b经过点A,且与x轴交于点B,当∠PAC=∠PAB时,求直线AB的解析式.
【答案】(1)m=-4;(2)y=![]() x+3,y=-
x+3,y=-![]() x+1
x+1
【解析】
(1)将点A,C的坐标代入反比例函数解析式中,即可得出结论;(2)分点B在AP的左侧和右侧两种情况,分别求出直线AC和AC'的解析式即可得出结论.
(1)∵点A(-2,a),C(3a-10,1)是反比例函数![]() 上,
上,
∴-2a=3a-10,
解得:a=2,
∴A(-2,2),C(-4,1),
∴m=-4;
(2)分两种情况讨论:
①当点B在AP左侧时,
∵∠PAC=∠PAB,
∴A、C、B三点共线,
将A(-2,2),C(-4,1)代入y=kx+b,并解得:
k=![]() ,b=3,
,b=3,
即直线AB的解析式为:y=![]() x+3;
x+3;
②当点B在AP右侧时,
∵∠PAC=∠PAB,
∴此时直线AB与①中的直线AB关于直线AP成轴对称,
此时k=-![]() ,
,
将(-2,2)代入y=-![]() x+b,得:b=1,
x+b,得:b=1,
即直线AB的解析式为:y=-![]() x+1;
x+1;
综上所述,直线AB的解析式为:y=![]() x+3,y=-
x+3,y=-![]() x+1.
x+1.


科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿BC所在直线平移得到△DEF.
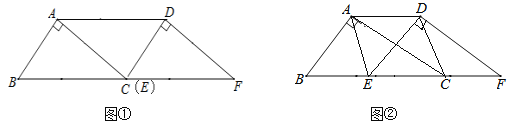
(1)如图①,当点E移动到点C处时,连接AD,求证:△CDA≌△ABC;
(2)如图②,当点E移动到BC中点时,连接AD、AE、CD,请你判断四边形AECD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
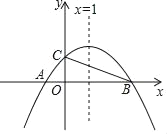
【题目】如图,已知抛物线y=ax2+bx+1与x轴相交于点A,B,与y轴相交于点C,点A的坐标为(﹣1,0),对称轴为直线x=1.
(1)求点B的坐标及抛物线的解析式;
(2)在直线BC上方的抛物线上有一点P,使△PBC的面积为1,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
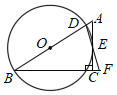
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.
(1)求证:BD=BF;
(2)填空:
①若⊙O的半径为5,tanB=![]() ,则CF= ;
,则CF= ;
②若⊙O与BF相交于点H,当∠B的度数为 时,四边形OBHE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
查看答案和解析>>
科目:初中数学 来源: 题型:
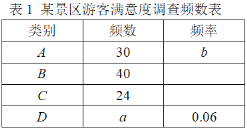
【题目】为了解游客对某景区的满意度,特对游客采取随机抽样的方式进行问卷调查,调查的结果分为A,B,C,D四类,其含意依次表示为“非常满意”、“比较满意”、“基本满意”和“不太满意”,划分类别后的数据整理如表1(不完整).
(1)求表中的数据a和b.
(2)如果根据表中频数画扇形统计图,那么类别为B的频数所对应的扇形圆心角是几度?
(3)已知该景区每日游客限流3000名,估计一天的游客中类别C的游客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
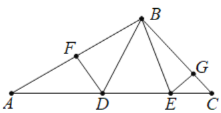
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,以点B为圆心,适当长为半径画弧交边于D,E两点(按照A,D,E,C依次排列,且D、E不重合).过D、E分别作AB和BC的垂线段交于F、G两点,如果线段DF=x,EG=y,则x、y的关系式为( )
A.20x-15y=![]() B.20x-15y=
B.20x-15y=![]()
C.15x-20y=![]() D.15x-20y=
D.15x-20y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.![]() ,
,![]() .
.
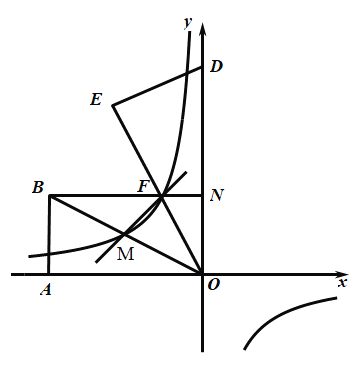
(1)求经过点![]() 、
、![]() 的反比例函数
的反比例函数![]() 和直线
和直线![]() :
:![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 轴,求五边形
轴,求五边形![]() 的面积;
的面积;
(3)直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com