
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() .连接
.连接![]() 、
、![]() 、
、![]() .在此运动变化的过程中,下列结论:①
.在此运动变化的过程中,下列结论:①![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() 长度的最小值为4;③四边形
长度的最小值为4;③四边形![]() 的面积保持不变;④
的面积保持不变;④![]() 面积的最大值为8.其中正确的结论是( )
面积的最大值为8.其中正确的结论是( )
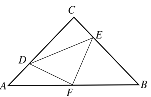
A.①②③B.①②④C.①③④D.②③④
【答案】C
【解析】
连接CF,根据全等三角形判定和性质可得①正确;由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小,可得②错误;由△ADF≌△CEF,得S△CEF=S△ADF,S四边形CEFD=S△AFC,得③正确;当△CEF面积最大时,由②③知,此时△DEF的面积最小,此时S△CEF=S四边形CEFD-S△DEF=S△AFC-S△DEF,可得④正确.
连接CF;
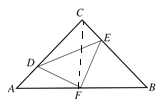
∵△ABC是等腰直角三角形,![]() 是
是![]() 边上的中点
边上的中点
∴∠FCB=∠A=45°,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF;
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形.
因此①正确.
由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;
即当DF⊥AC时,DE最小,此时DF=![]() BC=4.
BC=4.
∴DE=![]() =
=![]() DF=4
DF=4![]() ;
;
因此②错误.
∵△ADF≌△CEF,
∴S△CEF=S△ADF
∴S四边形CEFD=S△AFC,
因此③正确.
当△CEF面积最大时,由②③知,此时△DEF的面积最小.
此时S△CEF=S四边形CEFD-S△DEF=S△AFC-S△DEF=16-8=8;
因此④正确.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如果P 是正方形ABCD 内的一点,且满足∠APB+∠DPC=180°,那么称点P 是正方形 ABCD 的“对补点”.
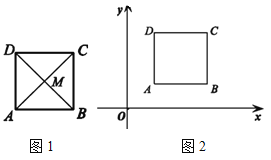
(1)如图1,正方形ABCD 的对角线AC,BD 交于点M,求证:点M 是正方形ABCD 的对补点;
(2)如图2,在平面直角坐标系中,正方形ABCD 的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
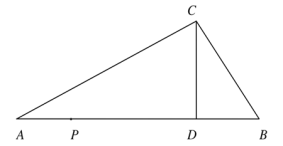
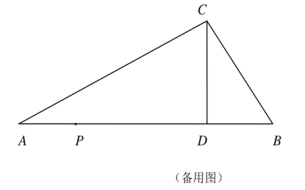
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 边上的高
边上的高![]() .
.
(1)![]() ;
;![]() .
.
(2)动点![]() 从
从![]() 出发,向终点
出发,向终点![]() 运动,速度为3个单位/秒,运动时间为
运动,速度为3个单位/秒,运动时间为![]() 秒.
秒.
①当![]() 为何值时,
为何值时,![]() ?
?
②当![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一副扑克牌中,拿出黑桃![]() 、黑桃
、黑桃![]() 、黑桃
、黑桃![]() 、黑桃
、黑桃![]() 四张牌,小刚从中堆积摸出一张记下牌面上的数字为
四张牌,小刚从中堆积摸出一张记下牌面上的数字为![]() ,再由小明从剩下的牌中随机摸出一张,记下牌面上的数字为
,再由小明从剩下的牌中随机摸出一张,记下牌面上的数字为![]() ,组成一对数
,组成一对数![]() .
.
(1)用列表法或树状图表示处![]() 的所有可能出现的结果;
的所有可能出现的结果;
(2)求小刚、小明各摸一次扑克牌所确定的一对数是方程![]() 的解的概率.
的解的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行收费标准如下: 
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com