
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ��� ![]() ��
�� ![]() �Ḻ�����ϣ�����
�Ḻ�����ϣ�����![]() ��
��![]() ���������ϣ�����
���������ϣ����� ![]() �ڵ�һ���ޣ��߶�
�ڵ�һ���ޣ��߶� ![]() ��
��![]() �ij���һԪ���η���
�ij���һԪ���η��� ![]() ��������
��������![]() ��
��![]() ��
��
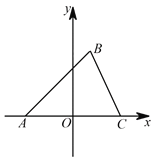
��1��ֱ��д����![]() ������ �� C ������ ��
������ �� C ������ ��
��2��������������![]() ��ͼ����
��ͼ����![]() ����
���� ![]() ��ֵ��
��ֵ��
��3����ͼ����![]() ��
��![]() ���ڵ�
���ڵ� ![]() ����
����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ� ![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ���������������
���������������![]() ��
��![]() ��
��![]() Ϊ���������������?�����ڣ�ֱ��д�����������ĵ�
Ϊ���������������?�����ڣ�ֱ��д�����������ĵ�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��������
����3��������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
��������
��1����һԪ���η���x2-12x+36=0������������ɵõ���A��C�����ꣻ
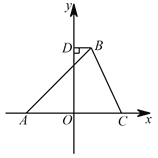
��2������B��BE��AC������ΪE���ɡ�BAC=45����֪AE=BE����BE=x���ù��ɶ����ɵ�CE=![]() ������AE+CE=OA+OC���ⷽ�����BE������AE-OA=OE�����������B�����꣬Ȼ�����k��ֵ��
������AE+CE=OA+OC���ⷽ�����BE������AE-OA=OE�����������B�����꣬Ȼ�����k��ֵ��
��3���������ۣ��������������ζ�Ӧ�߳ɱ��������P�����꣮
��1����һԪ���η��� ![]() ��
��
��ã�![]() ��
��
���� ![]() ��
��
���� ![]() ��
��![]() ��
��
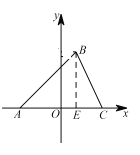
��2�� ��ͼ������ ![]() ��
�� ![]() ������Ϊ
������Ϊ ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
��![]() ��
��
�� ![]() =12��
=12��
�� EC=12-x��
��Rt��BEC����![]() ��
��
�� ![]()
�����ã�![]() ��
��
��ã�![]() ������������ȥ����
������������ȥ����![]() ��
��
�� ![]() ��
��![]() ��
��
�� ![]() ��
��

��![]() ����
����![]() ����
���� ![]() ��
��
��3�����ڣ�
��ͼ2��
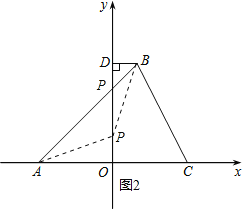
����P��OD�ϣ�����PDB�ס�AOP��
��![]() ����
����![]() ��
��
��ã�OP=2��OP=6��
��P��0��2����P��0��6����
��ͼ3��

����P��OD�Ϸ�����PDB�ס�AOP��
��![]() ����
����![]() ��
��
��ã�OP=12��
��P��0��12����
��ͼ4��
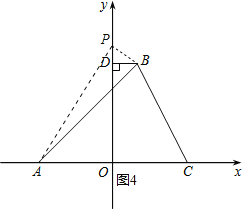
����P��OD�Ϸ�����BDP�ס�AOP��
��![]() ����
����![]() ��
��
��ã�OP=4+2![]() ��OP=4-2
��OP=4-2![]() ������������ȥ����
������������ȥ����
��P��0��4+2![]() ����
����
��ͼ5��
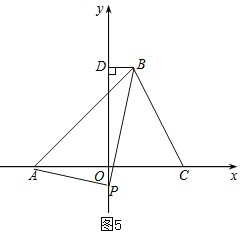
����P��y�Ḻ���ᣬ��PDB�ס�AOP��
��![]() ����
����![]() ��
��
��ã�OP=-4+2![]() ��-4-2
��-4-2![]() ������������ȥ����
������������ȥ����
��P��������0��4-2![]() ��
��
�ʵ� ![]() ������Ϊ��
��������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0��ͼ����ͼ�����н��ۣ�
��abc��0����3a+c��0����a+b��am2+bm����a��b+c��0������ax12+bx1=ax22+bx2����x1��x2����x1+x2=2��
������ȷ���У�����������
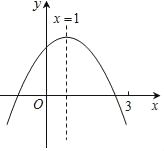
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���ACB=90�㣬AC=BC=2����ֱ�DZ�AC��A����ʱ����ת��AC��������BC�䣬EΪBC�����е㣬����CE,��CE�����ֵΪ( ).
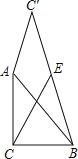
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������֪ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ��
��![]() ��
��![]() ����ֱ����һ�㣮
����ֱ����һ�㣮
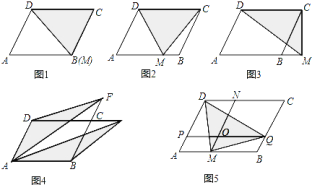
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() ________��
________��
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() ��
��![]() �����غ�ʱ��
�����غ�ʱ��![]() ________��
________��
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() ����
����![]() �����ӳ���ʱ��
�����ӳ���ʱ��![]() ________��
________��
��չ�ƹ㣺��ͼ![]() ��ƽ���ı���
��ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ӳ��������㣬����
�ӳ��������㣬����![]() ��
��![]() ��
��![]() ��
��![]() �����ͼ����Ӱ���ֵ��������˵�����ɣ�
�����ͼ����Ӱ���ֵ��������˵�����ɣ�
ʵ��Ӧ�ã���ͼ��һƽ���ı����̵�![]() ��
��![]() ��
��![]() �ֱ�ƽ����
�ֱ�ƽ����![]() ��
��![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ֽ����̵ظ��죬���̵��ڲ���һ������������
���ֽ����̵ظ��죬���̵��ڲ���һ������������![]() ������
������![]() ��
��![]() ��
��![]() ��ͼ����Ӱ���֣���ֲ��ͬ�Ļ��ݣ��������������������
��ͼ����Ӱ���֣���ֲ��ͬ�Ļ��ݣ��������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��BD��AC���ϵ����ߣ�AE��BC������Ϊ��E����BD��F��cos��ABC=![]() ��AB=13��
��AB=13��
��1����AE�ij���
��2����tan��DBC��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��1��0����B��1��a��0����C��1+a��0����a��0������P����D��4��4��ΪԲ�ģ�1Ϊ�뾶��Բ���˶�����ʼ�������BPC=90�㣬��a�����ֵ�ǣ� ��
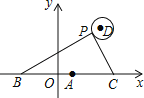
A. 3 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������ΪE������DE��FΪ�߶�DE��һ�㣬����AFE=��B

��1����֤����ADF�ס�DEC��
��2����AB=8��AD=6![]() ��AF=4
��AF=4![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
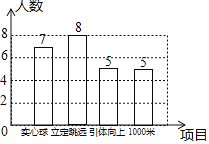
����Ŀ��ijѧУΪ���˽�����������������涨�μӲ��Ե�ÿ����������ʵ����������������Զ���������������������;���1000�����ĸ���Ŀ�������ȡһ����Ϊ������Ŀ��
��1�����꣨1�����25�����������μӣ��μӸ��������Ŀ��ͳ�ƽ����ͼ���μ���ʵ���������Ե������������� ���ˣ�
��2�����꣨1������8�������μ�����������Զ���IJ��ԣ����ǵijɼ�����λ���֣����£�95��100��82��90��89��90��90��85
����95��100��82��90��89��90��90��85���������ݵ��������� ������λ������ ����
��С��ͬѧ�ijɼ���92�֣����ijɼ���Σ�
�������������90�ֵijɼ���Ϊ���㣬������ư��꼶80����������������Զ���ɼ�Ϊ�����ѧ��ԼΪ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD����ͼʾ��ʽ�ֳɾŲ��֣���a��b�仯�Ĺ����У�����˵����ȷ���У� ��
��ͼ�д��������ֵ��ܳ�֮��ǡ�õ��ڳ�����ABCD���ܳ�
��������ABCD�ij���֮�ȿ���Ϊ2
����������ABCDΪ������ʱ���Ų��ֶ�Ϊ������
����������ABCD���ܳ�Ϊ60ʱ�������������Ϊ100

A.�٢�B.�٢�C.�ڢۢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com