
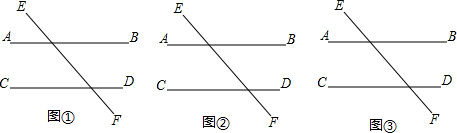
分析 (1)结论PM∥QN,欲证明PM∥NQ只要证明∠EMP=∠ENQ即可.
(2)结论PM∥NQ,欲证明PM∥NQ只要证明∠PMN=∠MNQ即可.
(3)结论:PM⊥NQ,欲证明PM⊥QN只要证明∠PMN+∠QNM=90°即可.
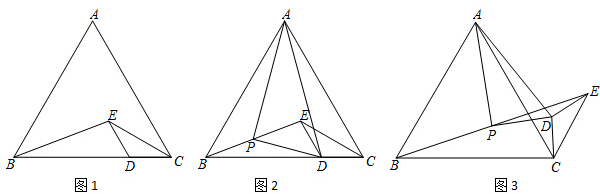
解答 (1)解:如图①中,结论MP∥NQ.
理由:∵AB∥DC,
∴∠EMB=∠END,
∵∠EMP=$\frac{1}{2}$∠EMB,∠ENQ=$\frac{1}{2}$∠END,
∴∠EMP=∠ENQ,
∴MP∥NQ.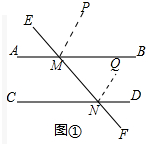
(2)如图②中,结论PM∥NQ,
理由::∵AB∥DC,
∴∠AMF=∠MND,
∵∠PMN=$\frac{1}{2}$∠AMF,∠MNQ=$\frac{1}{2}$∠MND,
∴∠PMN=∠MNQ,
∴MP∥NQ.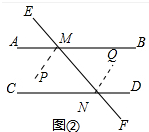
(3)如图③中,结论PM⊥PN,
理由:∵AB∥CD,
∴∠AMN+∠CNM=180°,
∵∠PMN=$\frac{1}{2}$∠AMN,∠QNM=$\frac{1}{2}$∠CNM,
∴∠PMN+∠QNM=90°,
∴∠MHN=90°,
∴PM⊥QN.
点评 本题考查平行线的性质,熟练应用平行线的性质是解决问题的关键,记住题目中的三个结论对以后解题是有帮助的,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
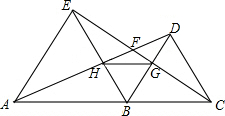 已知点A、B、C三点共线,分别以线段AB、BC为边作等边△ABE,△DBC,连接AD、EC.
已知点A、B、C三点共线,分别以线段AB、BC为边作等边△ABE,△DBC,连接AD、EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4<a<16 | B. | 14<a<26 | C. | 12<a<20 | D. | 8<a<32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形网格中的每个小正方形边长都1,每个小格的顶点叫做格点,以格点为顶点按下列要求画三角形.
正方形网格中的每个小正方形边长都1,每个小格的顶点叫做格点,以格点为顶点按下列要求画三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com