
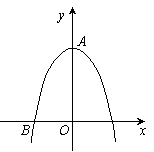
如图11,抛物线y=ax2 + c经过点A(0,2)和点B( -1,0).
-1,0).
(1)求此抛物线的解析式;
(2)将此抛物线平移,使其顶点坐标为(2,1),平移后的抛物线与x轴的两个交点分别为点C,D(点C在点D的左边),求点C,D的坐标;
(3)将此抛物线平移,设其顶点的纵坐标为m,平移后的抛物线与x轴两个交点之间的距离为n,若1<m<3,直接写出n的取 值范围.
值范围.
 |
科目:初中数学 来源: 题型:
学期初,学校体育组对九年级某班50名学生进行了跳远测试(满分5分),根据测试成绩制作了下面两个统计图(信息不完整)。
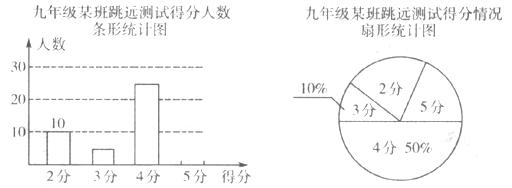
根据统计图解答下列问题:
(1)请补全条形统计图;
(2)本次测试的平均分是多少?
(3)通过一段时间的训练,体育组对该班50名学生进行第二次跳远测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中,得4分、5分的学生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
有一个数学游戏,其规则是:对一个“数串”中任意相邻的两个数, 都用右边的数减去左边的数,所得之差写在这两个数之间,产生一个新“数串”,这称为一次操作.例如:对于数串2,7,6,第一次操作后产生的新数串为2,5,7,-1,6;对产生的新数串进行同样的操作,第二次操作后产生的新数串为2,3,5,2,7,-8,-1,7,6;……对数串3,1,6也进行这样的操作,第30次操作后所产生的那个新数串中所有数的和是________.
都用右边的数减去左边的数,所得之差写在这两个数之间,产生一个新“数串”,这称为一次操作.例如:对于数串2,7,6,第一次操作后产生的新数串为2,5,7,-1,6;对产生的新数串进行同样的操作,第二次操作后产生的新数串为2,3,5,2,7,-8,-1,7,6;……对数串3,1,6也进行这样的操作,第30次操作后所产生的那个新数串中所有数的和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
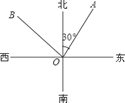
如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是( )
A.西偏北30° B .北偏西60°
.北偏西60°
C.北偏东30° D.东偏北60°
查看答案和解析>>
科目:初中数学 来源: 题型:
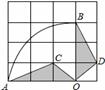
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则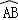 的长为( )
的长为( )
A.π B.6π C.3π D.1.5π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com