
【题目】如图,![]() ,
,![]() ,AE平分
,AE平分![]() ,
,![]() ,交AC延长线于F,且垂足为E,则下列结论:
,交AC延长线于F,且垂足为E,则下列结论:![]() ;
;![]() ;
;![]() ,
,![]() ;
;![]() 其中正确的结论有______
其中正确的结论有______![]() 填写序号
填写序号![]()

【答案】①③⑤
【解析】
试题根据∠ACB=90°,BF⊥AE,得出∠ACB=∠BED=∠BCF=90°,推出∠F=∠ADC,证△BCF≌△ACD,根据全等三角形的性质即可判断①②;假如AC+CD=AB,求出∠F+∠FBC≠90°,和已知矛盾,即可判断③④,证根据全等三角形的判定ASA得出△BEA≌△FEA,推出BE=EF,即可判断⑤.
解:∵∠ACB=90°,BF⊥AE,
∴∠ACB=∠BED=∠BCF=90°,
∴∠F+∠FBC=90°,∠BDE+∠FBC=90°,
∴∠F=∠BDE,
∵∠BDE=∠ADC,
∴∠F=∠ADC,
∵AC=BC,
∴△BCF≌△ACD,
∴AD=BF,∴①正确;②错误;
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
假如AC+CD=AB,
∴AB=AF,∴∠F=∠FBA=65°,
∴∠FBC=65°﹣45°=20°,
∴∠F+∠FBC≠90°,∴③错误;④错误;
由△BCF≌△ACD,
∴AD=BF,
∵AE平分∠BAF,AE⊥BF,
∴∠BEA=∠FEA=90°,∠BAE=∠FAE,
∵AE=AE,∴△BEA≌△FEA,
∴BE=EF,
∴⑤正确;
故答案为:①③⑤.


科目:初中数学 来源: 题型:
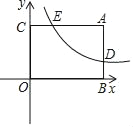
【题目】如图所示,已知矩形ABOC中,AC=4,双曲线y=![]() 与矩形两边AB、AC分别交于D、E,E为AC边中点.
与矩形两边AB、AC分别交于D、E,E为AC边中点.
(1)求点E的坐标;
(2)点P是线段OB上的一个动点,是否存在点P,使∠DPC=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
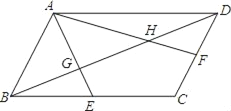
【题目】如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC.CD上的点且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE连结AG,先证明△ABE≌△ADG.再证明____≌____,可得出结论,他的结论应是____.请你按照小王同学的思路写出完整的证明过程.

实际应用
(2)如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处.且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离是 海里(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将直角三角板ABC绕直角顶点C逆时针旋转角度![]() ,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角
,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=∠ADB=90°,M、N 分别是 AB、CD 的中点.

(1)求证:MN⊥CD;
(2)若 AB=50,CD=48,求 MN 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com