
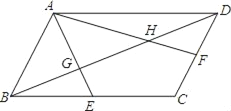
【题目】如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设△AGH的面积为S1,平行四边形ABCD的面积为S2,则S1:S2的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
因为四边形ABCD是平行四边形,所以AD∥BC,所以△AGD∽△EGB,由相似三角形的性质和已知条件可得:BG:GD=BE:AD=1:2,同理可证明△AHB∽FHD,由相似的性质可得:DH:HB=DF:AB=1:2,即G,H是BD三等分点,所以![]() 又因为S△ABE=
又因为S△ABE=![]() S平行四边形ABCD,所以S平行四边形ABCD
S平行四边形ABCD,所以S平行四边形ABCD![]() 即可求解.
即可求解.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AGD∽△EGB,
∵E,F分别是平行四边形ABCD边BC,CD中点,
∴BG:GD=BE:AD=1:2,
同理△AHB∽FHD,
∴DH:HB=DF:AB=1:2,
∴![]()
同理:![]()
∴BG=DH=GH,
即G,H是BD三等分点,
∴![]()
∵AH:HF=2:1,
∴AG:GE=2:1,
∴![]()
又∵S△ABE=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S平行四边形ABCD![]()
![]()
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
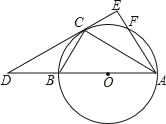
【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是![]() 的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是 , ;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于 度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3![]() 时,请直接写出线段CF的长的最大值是
时,请直接写出线段CF的长的最大值是

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家园林公司承接了某项园林绿化工程,己知乙公司单独完成此项工程所需要的天数是甲公司单独完成所需要天数的1.5倍,如果甲公司先单独工作10天,再由乙公司单独工作l5天,这样恰好完成整个工程的![]() ;
;
(1)求甲、乙两公司单独完成这项工程各需多少天?
(2)园林部门要求完成该绿化工程的时间不得超过30天,甲、乙公司合作若干天后,甲公司另有项目离开,剩下的工程由乙公司单独完成,求甲、乙两公司至少合作多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来
根据以上信息,解答下列问题:
(1)设租车时间为![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中![]() 、
、![]() 分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
(1)根据图象,求乙的行驶速度.
(2)解释交点A的实际意义.
(3)求甲出发多少时间,两人之间恰好相距5km?


查看答案和解析>>
科目:初中数学 来源: 题型:
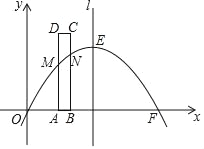
【题目】如图,已知抛物线y=ax2+bx与x轴分别交于原点O和点F(10,0),与对称轴l交于点E(5,5).矩形ABCD的边AB在x轴正半轴上,且AB=1,边AD,BC与抛物线分别交于点M,N.当矩形ABCD沿x轴正方向平移,点M,N位于对称轴l的同侧时,连接MN,此时,四边形ABNM的面积记为S;点M,N位于对称轴l的两侧时,连接EM,EN,此时五边形ABNEM的面积记为S.将点A与点O重合的位置作为矩形ABCD平移的起点,设矩形ABCD平移的长度为t(0≤t≤5).
(1)求出这条抛物线的表达式;
(2)当t=0时,求S△OBN的值;
(3)当矩形ABCD沿着x轴的正方向平移时,求S关于t(0<t≤5)的函数表达式,并求出t为何值时,S有最大值,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com