练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将一次函数（为常数）的图像位于轴下方的部分沿轴翻折到轴上方，和一次函数（为常数）的图像位于轴及上方的部分组成“”型折线，过点作轴的平行线，若该“”型折线在直线下方的点的横坐标满足，则的取值范围是（ ）

    A.B.C.D.

    【答案】A

    【解析】

    先解不等式3x+b＜1时，得x＜；再求出函数y=3x+b沿x轴翻折后的解析式为y=-3x-b，解不等式-3x-b＜1，得x＞-；根据x满足0＜x＜3，得出-=0，=3，进而求出b的取值范围．

    ∵y=3x+b，

    ∴当y＜1时，3x+b＜1，解得x＜；

    ∵函数y=3x+b沿x轴翻折后的解析式为-y=3x+b，即y=-3x-b，

    ∴当y＜1时，-3x-b＜1，解得x＞-；

    ∴-＜x＜，

    ∵x满足0＜x＜3，

    ∴-=0，=3，

    ∴b=-1，b=-8，

    ∴b的取值范围为-8≤b≤-1．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

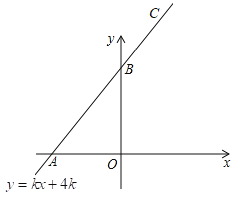
    【题目】如图，一次函数的图像与轴交于点，与轴交于点，且经过点．

    (1)当时；

    ①求一次函数的表达式；

    ②平分交轴于点，求点的坐标；

    (2)若△为等腰三角形，求的值；

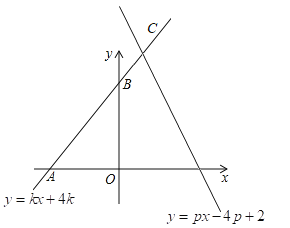
    (3)若直线也经过点，且，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用一条24cm的细绳围成一个等腰三角形。

    （1）如果腰长是底边的2倍，那么各边的长是多少？

    （2）能围成有一边长为4cm的等腰三角形吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点是正方形内一点，连接、、，若，，，则正方形的边长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

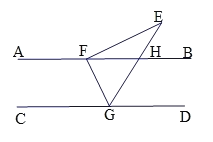
    【题目】如图，AB// CD，Rt△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，∠EFG=90°，∠E=32°．

    （1）∠FGE=　　　　°

    （2）若GE平分∠FGD，求∠EFB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

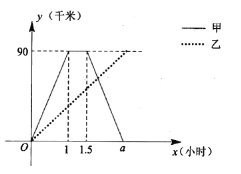
    【题目】甲、乙两人同时从相距千米的地匀速前往地，甲乘汽车，乙骑电动车，甲到达地停留半个小时后按原速返回地，如图是他们与地之间的距离（千米）与经过的时间（小时）之间的函数图像．

    （1） ，并写出它的实际意义 ；

    （2）求甲从地返回地的过程中与之间的函数表达式，并写出自变量的取值范围；

    （3）已知乙骑电动车的速度为千米/小时，求乙出发后多少小时与甲相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

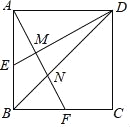
    【题目】正方形ABCD的边长AB=2，E为AB的中点，F为BC的中点，AF分别与DE、BD相交于点M，N，则MN的长为（　　）

    A. B. ﹣1 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论，其中不正确的结论是（ ）

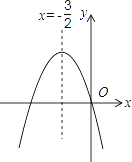
    A. abc=0 B. a+b+c＞0 C. 3a=b D. 4ac﹣b2＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠A=∠D=90°，点E、F在线段BC上，DE与AF交于点O，且AB=DC，BE=CF．求证：

    （1）AF=DE

    （2）若OP⊥EF，求证：OP平分∠EOF．

    查看答案和解析>>

    同步练习册答案