
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点.
,D是BC的中点.
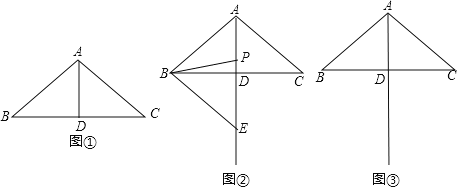
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转![]() ,点B的对应点是点E,连接BE,得到
,点B的对应点是点E,连接BE,得到![]() .小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①![]() ;②连接CE,直线CE与直线AB的位置关系是 .
;②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出![]() ,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
【答案】(1)①50![]() ;②
;②![]() ;(2)
;(2)![]() ;(3)AE的最小值
;(3)AE的最小值![]() .
.
【解析】
(1)①利用等腰三角形的性质即可解决问题.②证明![]() ,
,![]() ,推出
,推出![]() 即可.
即可.
(2)如图③中,以P为圆心,PB为半径作⊙P.利用圆周角定理证明![]() 即可解决问题.
即可解决问题.
(3)因为点E在射线CE上运动,点P在线段AD上运动,所以当点P运动到与点A重合时,AE的值最小,此时AE的最小值![]() .
.
(1)①如图②中,
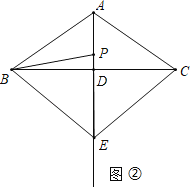
∵![]() ,
,![]() ,
,
∴![]() ,
,
②结论:![]() .
.
理由:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AE垂直平分线段BC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为50,![]() .
.
(2)如图③中,以P为圆心,PB为半径作⊙P.

∵AD垂直平分线段BC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ![]() .
.
(3)如图④中,作![]() 于H,
于H,
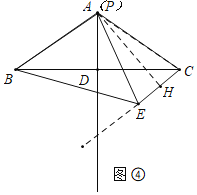
∵点E在射线CE上运动,点P在线段AD上运动,
∴当点P运动到与点A重合时,AE的值最小,此时AE的最小值![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店![]() 两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.
两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.
(1)求该店平均每天销售这两种湘莲礼盒各多少盒?
(2)小亮调査发现,![]() 种湘莲礼盒售价每降3元可多卖1盒.若
种湘莲礼盒售价每降3元可多卖1盒.若![]() 种湘莲礼盒的售价和销量不变,当
种湘莲礼盒的售价和销量不变,当![]() 种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?
种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、B两点,与x轴交于点C,与y轴交于点E,其中
、B两点,与x轴交于点C,与y轴交于点E,其中![]() .
.
![]() 求该一次函数和反比例函数的解析式;
求该一次函数和反比例函数的解析式;
![]() 若点D是x轴正半轴上一点,且
若点D是x轴正半轴上一点,且![]() ,连接OB、BD,求
,连接OB、BD,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
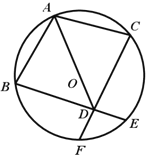
【题目】已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.
(1)求证:BD=CD:
(2)如果AB2=AO·AD,求证:四边形ABDC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(探究发现)
如图1,![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 两条对角线的交点处,
两条对角线的交点处,![]() ,将
,将![]() 绕点
绕点![]() 旋转,旋转过程中,
旋转,旋转过程中,![]() 的两边分别与正方形
的两边分别与正方形![]() 的边
的边![]() 和
和![]() 交于点
交于点![]() 和点
和点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合).则
不重合).则![]() 之间满足的数量关系是 .
之间满足的数量关系是 .
(2)(类比应用)
如图2,若将(1)中的“正方形![]() ”改为“
”改为“![]() 的菱形
的菱形![]() ”,其他条件不变,当
”,其他条件不变,当![]() 时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)(拓展延伸)
如图3,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() ,且
,且![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
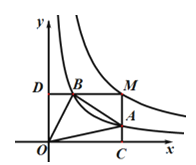
【题目】反比例函数![]() ,a为常数)和
,a为常数)和![]() 在第一象限内的图象如下左图所示,点M在
在第一象限内的图象如下左图所示,点M在![]() 的图象上,MC⊥x轴于点C,交
的图象上,MC⊥x轴于点C,交![]() 的图象于点A,MD⊥y轴于点D,交
的图象于点A,MD⊥y轴于点D,交![]() 的图象于点B,若
的图象于点B,若![]() ,则
,则![]() = _____________.
= _____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上任取一点M(![]() )、把线段MB绕M点逆时针旋转90°至MC.连接AC,作AC的垂直平分线交AM于N点,此时AN、MN、BM为边的三角形是一个直角三角形,我们称点M,N是线段AB的勾股分割点.如下右图,已知:点M,N是线段AB的勾股分割点,
)、把线段MB绕M点逆时针旋转90°至MC.连接AC,作AC的垂直平分线交AM于N点,此时AN、MN、BM为边的三角形是一个直角三角形,我们称点M,N是线段AB的勾股分割点.如下右图,已知:点M,N是线段AB的勾股分割点,![]() ,△ABC、△MND分别是以AB、MN为斜边的等腰直角三角形,且点C与点D在AB的同侧,若MN=3,连接CD,则CD=______.
,△ABC、△MND分别是以AB、MN为斜边的等腰直角三角形,且点C与点D在AB的同侧,若MN=3,连接CD,则CD=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某户居民2018年的电费支出情况(每![]() 个月缴费
个月缴费![]() 次)如图所示:
次)如图所示:

根据以上信息,解答下列问题:
(1)求扇形统计图中“9﹣10月”对应扇形的圆心角度数;
(2)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com