
【题目】某政府工作报告中强调,2019年着重推进乡村振兴战略,做优做响湘莲等特色农产品品牌.小亮调查了一家湘潭特产店![]() 两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.
两种湘莲礼盒一个月的销售情况,A种湘莲礼盒进价72元/盒,售价120元/盒,B种湘莲礼盒进价40元/盒,售价80元/盒,这两种湘莲礼盒这个月平均每天的销售总额为2800元,平均每天的总利润为1280元.
(1)求该店平均每天销售这两种湘莲礼盒各多少盒?
(2)小亮调査发现,![]() 种湘莲礼盒售价每降3元可多卖1盒.若
种湘莲礼盒售价每降3元可多卖1盒.若![]() 种湘莲礼盒的售价和销量不变,当
种湘莲礼盒的售价和销量不变,当![]() 种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?
种湘莲礼盒降价多少元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是多少元?
【答案】(1)该店平均每天销售![]() 礼盒10盒,
礼盒10盒,![]() 种礼盒为20盒;(2)当
种礼盒为20盒;(2)当![]() 种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.
种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.
【解析】
(1)根据题意,可设平均每天销售![]() 礼盒
礼盒![]() 盒,
盒,![]() 种礼盒为
种礼盒为![]() 盒,列二元一次方程组即可解题
盒,列二元一次方程组即可解题
(2)根据题意,可设![]() 种礼盒降价
种礼盒降价![]() 元/盒,则
元/盒,则![]() 种礼盒的销售量为:(
种礼盒的销售量为:(![]() )盒,再列出关系式即可.
)盒,再列出关系式即可.
解:(1)根据题意,可设平均每天销售![]() 礼盒
礼盒![]() 盒,
盒,![]() 种礼盒为
种礼盒为![]() 盒,
盒,
则有![]() ,解得
,解得![]()
故该店平均每天销售![]() 礼盒10盒,
礼盒10盒,![]() 种礼盒为20盒.
种礼盒为20盒.
(2)设A种湘莲礼盒降价![]() 元/盒,利润为
元/盒,利润为![]() 元,依题意
元,依题意
总利润![]()
化简得![]()
∵![]()
∴当![]() 时,取得最大值为1307,
时,取得最大值为1307,
故当![]() 种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.
种湘莲礼盒降价9元/盒时,这两种湘莲礼盒平均每天的总利润最大,最大是1307元.


科目:初中数学 来源: 题型:
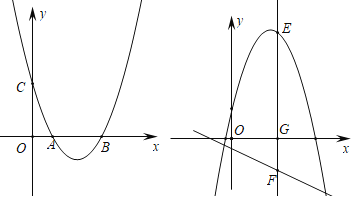
【题目】如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.
(1)求抛物线的表达式和顶点D的坐标;
(2)在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;
(3)将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=-![]() x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
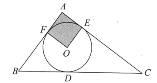
A.4B.6.25C.7.5D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
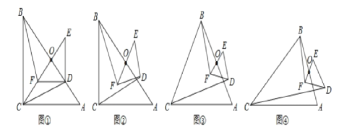
【题目】如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C, F, O在同一条直线上,可以证明△BOF≌△COD,则BF=CD,
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出![]() 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与![]() 轴相交于负半轴,下列结论:①
轴相交于负半轴,下列结论:①![]() ;②方程
;②方程![]() 的两根一个大于1,另一个小于-1;③
的两根一个大于1,另一个小于-1;③![]() ;④
;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
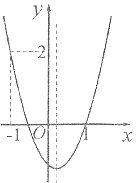
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片OABC放置在直角坐标系中,点A(3,0),点C(0,![]() ).
).
(I).如图,经过点O、B折叠纸片,得折痕OB,点A的对应点为![]() ,求
,求![]() 的度数;
的度数;
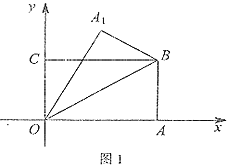
(Ⅱ)如图,点M、N分别为边OA、BC上的动点,经过点M、N折叠纸片,得折痕MN,点B的对应点为![]()
①当点B的坐标为(-1,0)时,请你判断四边形![]() 的形状,并求出它的周长;
的形状,并求出它的周长;
②若点N与点C重合,当点![]() 落在坐标轴上时,直接写出点M的坐标.
落在坐标轴上时,直接写出点M的坐标.
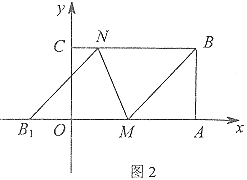
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
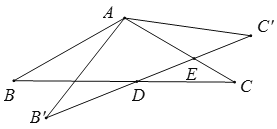
A. B.
B.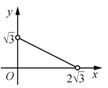 C.
C.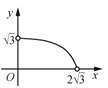 D.
D.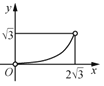
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点.
,D是BC的中点.
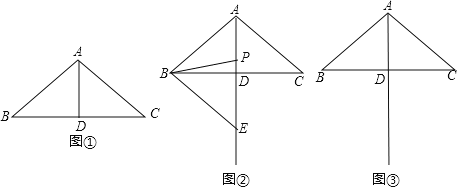
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转![]() ,点B的对应点是点E,连接BE,得到
,点B的对应点是点E,连接BE,得到![]() .小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①![]() ;②连接CE,直线CE与直线AB的位置关系是 .
;②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出![]() ,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com