
【题目】在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示.

(1)如图①,在△ABC中,∠A=2∠B,且∠A=60°.求证:a2=b(b+c)
(2)如图②,在△ABC中,最大角∠A是最小角∠C的2倍,且c=7,b=8,求a的长.
(3)若一个三角形的一个内角等于另一个内角的2倍,我们则称这样的三角形为“倍角三角形”.问题(1)中的三角形是一个特殊的倍角三角形,那么对于任意的倍角△ABC,如图③,∠A=2∠B,关系式a2=b(b+c)是否仍然成立?并证明你的结论.
【答案】(1)见解析;(2)a=![]() ;(3)关系式a2=b(b+c)仍然成立,见解析.
;(3)关系式a2=b(b+c)仍然成立,见解析.
【解析】
(1)先证△ACB为直角三角形,知a=![]() c,b=
c,b=![]() c,据此可得a2=(
c,据此可得a2=(![]() c)2=
c)2=![]() ,b(b+c)=
,b(b+c)=![]() c(
c(![]() c+c)=
c+c)=![]() ,从而得出答案;
,从而得出答案;
(2)延长CA至点D,使AD=AB,连接BD,证△CBD∽△DAB得![]() ,据此可得BD=
,据此可得BD=![]() ,由∠C=∠D知a=BC=BD=
,由∠C=∠D知a=BC=BD=![]() ;
;
(3)延长BA至D,使AD=AC=b,连结CD,证△ADC∽△CDB得![]() ,据此可得答案.
,据此可得答案.
解:(1)证明:∵∠A=2∠B=60°,
∴∠B=30°,
则∠C=180°﹣∠A﹣∠B=90°,
∴△ACB为直角三角形,
在Rt△ACB中a=![]() c,b=
c,b=![]() c,
c,
所以a2=(![]() c)2=
c)2=![]() ,b(b+c)=
,b(b+c)=![]() c(
c(![]() c+c)=
c+c)=![]() ,
,
所以a2=b(b+c);
(2)如图1,延长CA至点D,使AD=AB,连接BD,
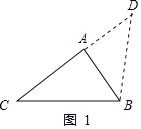
则∠D=∠ABD=![]() ∠CAB=∠C,
∠CAB=∠C,
∴△CBD∽△DAB,
∴![]() ,
,
∴BD2=ABCD=7×(8+7)=105,
∴BD=![]() ,
,
又∠C=∠D,
∴a=BC=BD=![]()
(3)对于任意的倍角△ABC,∠A=2∠B,关系式a2=b(b+c)仍然成立,
如图2,延长BA至D,使AD=AC=b,连结CD,
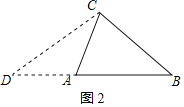
则∠CAB=2∠D,
∴∠B=∠D,BC=CD=a,
∴△ADC∽△CDB
∴![]() ,
,
即![]() .
.
所以a2=b(b+c).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
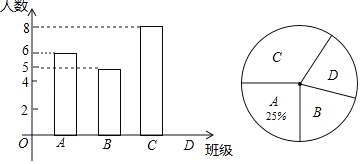
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
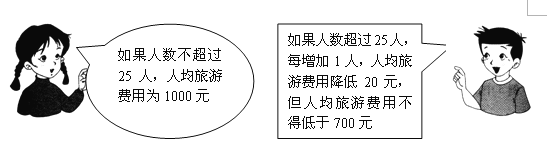 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
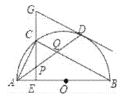
【题目】如图,在半⊙![]() 中,
中,![]() 是直径,点
是直径,点![]() 是⊙
是⊙![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() ,关于下列结论:①
,关于下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的外心;④
的外心;④![]() ,其中结论正确的是____.
,其中结论正确的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果记y=![]() =f(x),并且f(1)表示当x=1时y的值.即f(1)=
=f(x),并且f(1)表示当x=1时y的值.即f(1)=![]() =
=![]() ;f(
;f(![]() )表示当x=
)表示当x=![]() 时y的值,f(
时y的值,f(![]() )=
)=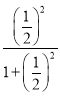 =
=![]() …,那么f(﹣1)+f(﹣2)+f(﹣
…,那么f(﹣1)+f(﹣2)+f(﹣![]() )+f(﹣3)+f(﹣
)+f(﹣3)+f(﹣![]() )+…+f(﹣2019)+f(﹣
)+…+f(﹣2019)+f(﹣![]() )=_____.
)=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可随机抽取一张奖劵,抽得奖券“紫气东来”、“花开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元.小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:

(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10 米),围成一个长方形的花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式;写出自变量x的取值范围.
(2)怎样围才能使长方形花圃的面积最大?最大值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ),经过点
),经过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(Ⅰ)求抛物线的解析式;
(Ⅱ)若点![]() 是射线
是射线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,交抛物线于点
,交抛物线于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,已知
,已知![]() ,
,![]() 是以
是以![]() 为未知数的一元二次方程
为未知数的一元二次方程![]() (
(![]() 为常数)的两个实数根,点
为常数)的两个实数根,点![]() 在抛物线上,连接
在抛物线上,连接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,求出
,求出![]() 值及点
值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展有奖问卷调查活动,并用得到的数据绘制了如下条形统计图(得分为整数,满分为10分,最低分为6分).请根据图中信息,解答下列问题:
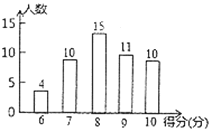
(Ⅰ)本次调查一共抽取了______名居民;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)如果对该小区的![]() 名居民全面开展这项有奖问答活动,得
名居民全面开展这项有奖问答活动,得![]() 分者设为一等奖,请你根据调查结果,帮社区工作人员估计需准备多少份一等奖奖品.
分者设为一等奖,请你根据调查结果,帮社区工作人员估计需准备多少份一等奖奖品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com