
【题目】已知:如图,C是线段AB上一点,分别以AC.BC为边作等边△DAC和等边△ECB,AE与BD.CD相交于点F、G,CE与BD相交于点H.
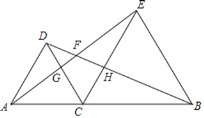
(1)求证:△ACE≌△DCB;
(2)求∠AFB的度数.
【答案】(1)见解析;(2)∠AFB=120°.
【解析】
(1)因为△DAC和△ECB均为等边三角形,则有AC=DC,CE=CB,∠ACD=∠ECB=60°,然后求出∠ACE=∠DCB,利用SAS即可证得△ACE≌△DCB;
(2)由全等三角形的性质和三角形内角和定理可得出结果.
解:(1)∵△DAC是等边三角形,
∴AC=DC,∠ACD=60°,
∵△BCE是等边三角形,
∴CE=CB,∠ECB=60°,
∴∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE和△BCD中,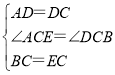 ,
,
∴△ACE≌△DCB(SAS);
(2)∵△ACE≌△DCB,
∴∠AEC=∠DBC,
又∵∠EHF=∠BHC,
∴∠EFH=∠BCH=60°,
∴∠AFB=180°60°=120°.


科目:初中数学 来源: 题型:
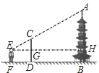
【题目】如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面![]() ,竹杆顶端离地面
,竹杆顶端离地面![]() ,小明到竹杆的距离
,小明到竹杆的距离![]() ,竹杆到塔底的距离
,竹杆到塔底的距离![]() ,求这座古塔的高度.
,求这座古塔的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作与探究:如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G点在边BC上,BG=10.
①第一次折叠:当折痕的另一端点F在AB边上时,如图1,求折痕GF的长;
②第二次折叠:当折痕的另一端点F在AD边上时,如图2,证明四边形BGEF为菱形,并求出折痕GF的长.

(2)拓展延伸:通过操作探究发现在矩形纸片ABCD中,AB=5,AD=13.如图3所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A′在BC边上可移动的最大距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线![]() .
.

对于抛物线![]() .
.
![]() 它与
它与![]() 轴交点的坐标为________,与
轴交点的坐标为________,与![]() 轴交点的坐标为________,顶点坐标为________.
轴交点的坐标为________,顶点坐标为________.
![]() 在所给的平面直角坐标系中画出此时抛物线;
在所给的平面直角坐标系中画出此时抛物线;
![]() 结合图象回答问题:当
结合图象回答问题:当![]() 时,
时,![]() 的取值范围是________.
的取值范围是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )

A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,光明中学一教学楼顶上竖有一块高为AB的宣传牌,点E和点D分别是教学楼底部和外墙上的一点(A,B,D,E在同一直线上),小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°,同时测得教学楼外墙外点D的仰角为30°,从点C沿坡度为1∶![]() 的斜坡向上走到点F时,DF正好与水平线CE平行.
的斜坡向上走到点F时,DF正好与水平线CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若在点F处测得宣传牌顶部A的仰角为45°,求出宣传牌AB的高度(结果精确到0.01).(注:sin67°≈0.92,tan67°≈2.36,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com