
【题目】(1)操作与探究:如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G点在边BC上,BG=10.
①第一次折叠:当折痕的另一端点F在AB边上时,如图1,求折痕GF的长;
②第二次折叠:当折痕的另一端点F在AD边上时,如图2,证明四边形BGEF为菱形,并求出折痕GF的长.

(2)拓展延伸:通过操作探究发现在矩形纸片ABCD中,AB=5,AD=13.如图3所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则点A′在BC边上可移动的最大距离是 .
【答案】(1)①GF=5![]() ;②4
;②4![]() ;(2)4.
;(2)4.
【解析】
(1)①首先利用翻折变换的性质以及勾股定理求出AE的长,进而利用勾股定理求出AF和EF的长,根据勾股定理即可得出结论;
②首先证明四边形BGEF是平行四边形,再利用BG=EG,得出四边形BGEF是菱形,再利用菱形性质求出FG的长;
(2)分别利用当点P与点B重合时,以及当点D与点Q重合时,求出A′B的极值进而得出答案.
(1)①解:如图①过G作GH⊥AD,
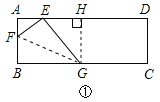
在Rt△GHE中,GE=BG=10,GH=8,
所以,EH=![]() =6,AE=10-6=4,
=6,AE=10-6=4,
设AF=x,则EF=BF=8-x,
则AF2+AE2=EF2,
∴x2+42=(8-x)2,
解得:x=3,
∴AF=3,BF=EF=5,
在Rt△BFG中,根据勾股定理得FG=![]() .
.
②证明:如图②,过F作FK⊥BG于K,

∵ABCD是矩形,
∴AD∥BC,BH∥EG,
∴四边形BGEF是平行四边形;
由对称性知,BG=EG,
∴四边形BGEF是菱形.
BG=BF=10,AB=8,AF=6,
∴KG=4,FG=![]() ;
;
(2)如图1,当点P与点B重合时,根据翻折对称性可得BA′=AB=5,
如图2,当点D与点Q重合时,根据翻折对称性可得
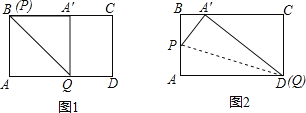
A′D=AD=13,
在Rt△A′CD中,A′D2=A′C2+CD2,
即132=(13-A′B)2+52,
解得:A′B=1,
所以点A'在BC上可移动的最大距离为5-1=4.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=12cm,AD=5cm,E是DC上一点(点E不与D、C重合)连接AE,以AE所在的直线为折痕,折叠纸片,点D的对应点为D′,点F为线段BC上一点,连接EF,以EF所在的直线为折痕折叠纸片,使点C的对应点C′落在直线ED′上,若CF=4时,DE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年来,为了缓减环境污染,某区加大了对煤改电的投资力度,该区居民在2015年有7500户完成煤改电,2017年有10800户完成了煤改电.
(1)求该区2015年至2017年完成煤改电户数的年平均增长率;
(2)2018年该区计划要完成煤改电的户数比2017年要有所增长,但增长率不超过15%,请求出2018年最多有多少户能完成煤改电.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 是
是![]() 的
的![]() 边上的中点,过点
边上的中点,过点![]() 的一条直线交
的一条直线交![]() 于
于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 于
于![]() ,我们可以证明
,我们可以证明![]() 成立(不要求考生证明).
成立(不要求考生证明).
![]() 如图
如图![]() ,若将图
,若将图![]() 中的过点
中的过点![]() 的一条直线交
的一条直线交![]() 于
于![]() ,改为交
,改为交![]() 的延长线于
的延长线于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,改为交
,改为交![]() 于
于![]() ,其它条件不变,则
,其它条件不变,则![]() 还成立吗?如果成立,请给出证明;如果不成立,请说出理由;
还成立吗?如果成立,请给出证明;如果不成立,请说出理由;
![]() 根据图
根据图![]() ,请你找出
,请你找出![]() 、
、![]() 、
、![]() 、
、![]() 四条线段之间的关系,并给出证明;
四条线段之间的关系,并给出证明;
![]() 如图
如图![]() ,若将图
,若将图![]() 中的过点
中的过点![]() 的一条直线交
的一条直线交![]() 于
于![]() ,改为交
,改为交![]() 的反向延长线于
的反向延长线于![]() ,交
,交![]() 的延长线于
的延长线于![]() ,改为交
,改为交![]() 于
于![]() ,其它条件不变,则
,其它条件不变,则![]() 得到的结论是否成立?
得到的结论是否成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴交点的横坐标为
轴交点的横坐标为![]() ,
,![]() ,则对于下列结论:
,则对于下列结论:
①当![]() 时,
时,![]() ;
;
②方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ;
;
③![]() .
.
其中正确的结论有________(只需填写序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是线段AB上一点,分别以AC.BC为边作等边△DAC和等边△ECB,AE与BD.CD相交于点F、G,CE与BD相交于点H.
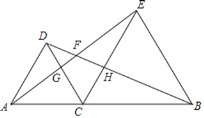
(1)求证:△ACE≌△DCB;
(2)求∠AFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,BE、CD相交于点O.

(1)若BD=CE,试说明:OB=OC.
(2)若BC=10,BC边上的中线AM=12,试求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com