
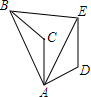
 如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=6,则BE=6.
如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=6,则BE=6. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
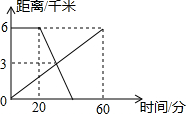 已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知:
已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | A | B |
| 成本(万元/套) | 30 | 40 |
| 售价(万元/套) | 35 | 47 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com