
 在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
|


科目:初中数学 来源: 题型:
 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.
光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、斜边对应相等的两个直角三角形全等 |
| B、底边对应相等的两个等腰三角形全等 |
| C、面积相等的两个等边三角形全等 |
| D、面积相等的两个长方形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(-x)2+2=(-x)4=x4 |
| B、-x2•(-x)2=-x2+2=-x4 |
| C、-x2•x2=-x2+2=-x4 |
| D、-x2•x2=-x2×2=-x4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
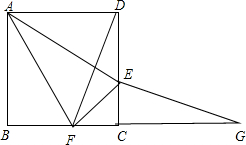 在正方形ABCD中,E、F分别是边CD、BC上的点,且CE=CF,点G是BC延长线上的一点且∠CEG+∠CDF=90°,连结EF、AE、AF.
在正方形ABCD中,E、F分别是边CD、BC上的点,且CE=CF,点G是BC延长线上的一点且∠CEG+∠CDF=90°,连结EF、AE、AF.查看答案和解析>>
科目:初中数学 来源: 题型:
 某校七(1)班全体同学喜欢的球类运动如图所示的统计图表示,下面说法正确的是( )
某校七(1)班全体同学喜欢的球类运动如图所示的统计图表示,下面说法正确的是( )| A、从图中可以直接看出喜欢各种球类的具体人数 |
| B、从图中可以直接看出全班的总人数 |
| C、从图中可以直接看出全班同学一学期来喜欢各种球类的变化情况 |
| D、从图中可以直接看出全班同学现在最喜欢各种球类人数的百分比 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com