
【题目】如图,函数y=x的图象与函数y![]() 的图象相交于点P(1,m).
的图象相交于点P(1,m).
(1)求 m,k 的值.
(2)直线 y=2与函数y=x的图象相交于点A,与函数y![]() 的图象相交于点B,求线段 AB 长.
的图象相交于点B,求线段 AB 长.
(3)直接写出不等式x![]() 的解集.
的解集.

科目:初中数学 来源: 题型:
【题目】台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?

![]()

![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,一次函数y=![]() x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
(1)求点A,B的坐标.
(2)如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.
(3)若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ,若存在,请求出对应的点Q坐标;若不存在,请说明理由.
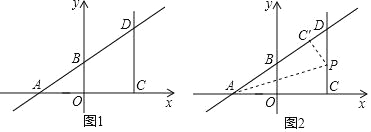
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 y=-x+b 与反比例函数y=![]() (x>0)的图象交于 A,B 两点,与 x 轴、y轴分别交于C,D 两点,连接 OA,OB,过 A 作 AE⊥x 轴于点 E,交 OB 于点F,设点 A 的横坐标为 m. 若 S△OAF+S 四边形 EFBC=4,则 m 的值是( )
(x>0)的图象交于 A,B 两点,与 x 轴、y轴分别交于C,D 两点,连接 OA,OB,过 A 作 AE⊥x 轴于点 E,交 OB 于点F,设点 A 的横坐标为 m. 若 S△OAF+S 四边形 EFBC=4,则 m 的值是( )
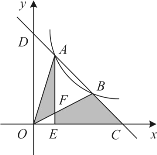
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
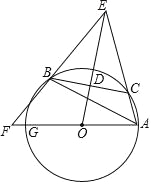
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
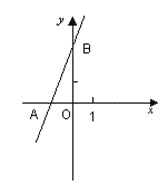
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AD∥BC,AB⊥AD,且AB=AD+BC,E是DC的中点,连结BE并延长交AD的延长线于G.
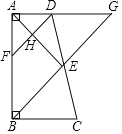
(1)求证:DG=BC;
(2)F是AB边上的动点,当F点在什么位置时,FD∥BG;说明理由.
(3)在(2)的条件下,连结AE交FD于H,FH与HD长度关系如何?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
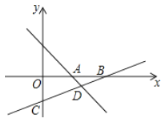
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
![]() 求直线
求直线![]() 的函数关系式;
的函数关系式;
![]() 点
点![]() 是
是![]() 上的一点,若
上的一点,若![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
![]() 设点
设点![]() 的坐标为
的坐标为![]() ,是否存在
,是否存在![]() 的值使得
的值使得![]() 最小?若存在,请求出点
最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com