
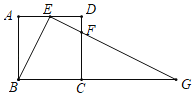
【题目】如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
【答案】(1)详见解析;(2)10
【解析】
(1)由正方形的性质得出∠A=∠D=90°,AB=BC=CD=AD,AD∥BC,证出∠ABE=∠DEF,即可得出△ABE∽△DEF;
(2)求出DF=1,CF=3,由相似三角形的性质得出![]() ,解得DE=2,证明△EDF∽△GCF,得出
,解得DE=2,证明△EDF∽△GCF,得出![]() ,求出CG=6,即可得出答案.
,求出CG=6,即可得出答案.
(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°,AB=BC=CD=AD,AD∥BC,
∵∠BEF=90°,
∵∠AEB+∠EBA=∠DEF+∠EBA=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF;
(2)解:∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3,
∵△ABE∽△DEF,
∴![]() ,即
,即![]() ,
,
解得:DE=2,
∵AD∥BC,
∴△EDF∽△GCF,
∴![]() ,即
,即![]() ,
,
∴CG=6,
∴BG=BC+CG=4+6=10.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】将一条长为![]() 的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
(1)要使这两个正方形的面积之和等于![]() ,那么这段铁丝剪成两段后的长度分别是多少?
,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于![]() 吗?若能,求出两段铁丝的长度;若不能,请说明理由。
吗?若能,求出两段铁丝的长度;若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据![]() ,3,
,3,![]() ,2,
,2,![]() 中可以作为线段AQ长的有_____个.
中可以作为线段AQ长的有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国青少年发展基金会为某地“希望小学”捐赠物资,其中文具和食品共320件,文具比食品多80件.
(1)求文具和食品各多少件;
(2)现计划租用甲、乙两种货车共8辆,一次性将这批文具和食品全部运往该地.已知甲种货车最多可装文具40件和食品10件,乙种货车最多可装文具和食品各20件.则中国青少年发展基金会安排甲、乙两种货车时有几种方案?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在△ABC中,点D在AB上,连接CD. DE平分∠BDC交BC于点E,且DE∥AC, 若F为AC的中点,连接DF.
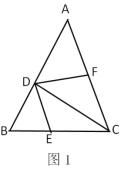
(1)求证:DF⊥DE.
(2)若BE:CE=2:3,S△CDE=9,求△ABC的面积.
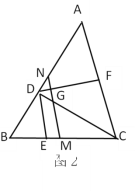
(3)如图2,M为BC的中点,过M作MN∥DE交AB于点N,交CD于点G,若BD=a,DG=b.试求CD的长(用a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
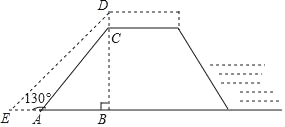
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程ax2+(a+2)x+9a=0有两个不等的实数根x1,x2,且x1<1<x2,那么a的取值范围是( )
A.﹣![]() <a<
<a<![]() B.a>
B.a>![]() C.a<﹣
C.a<﹣![]() D.﹣
D.﹣![]() <a<0
<a<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com