
【题目】将一条长为![]() 的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
(1)要使这两个正方形的面积之和等于![]() ,那么这段铁丝剪成两段后的长度分别是多少?
,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于![]() 吗?若能,求出两段铁丝的长度;若不能,请说明理由。
吗?若能,求出两段铁丝的长度;若不能,请说明理由。
【答案】(1)这段铁丝剪成两段后的长度分别是![]() 、
、![]() ;(2)两个正方形的面积之和不可能等于
;(2)两个正方形的面积之和不可能等于![]() . 理由见解析.
. 理由见解析.
【解析】
(1)这段铁丝被分成两段后,围成正方形.其中一个正方形的边长为![]() ,则另一个正方形的边长为
,则另一个正方形的边长为![]() ,根据“两个正方形的面积之和等于
,根据“两个正方形的面积之和等于![]() ”作为相等关系列方程,解方程即可求解;
”作为相等关系列方程,解方程即可求解;
(2)由(1)的方法列方程,根据方程无实数解即可得出结论.
解:(1)设其中一个正方形的边长为![]() ,则另一个正方形的边长为
,则另一个正方形的边长为![]() ,
,
依题意列方程得![]() ,
,
整理得![]() ,解得
,解得![]() ,
,![]() ,
,
∴两个正方形边长分别为1cm和5cm,
∴![]() ,
,![]() ;
;
![]() 这段铁丝剪成两段后的长度分别是
这段铁丝剪成两段后的长度分别是![]() 、
、![]() ;
;
(2)两个正方形的面积之和不可能等于![]() .
.
理由:由(1)可知![]() ,
,
化简后得![]() ,
,
![]() △
△![]() ,
,
![]() 方程无实数解;
方程无实数解;
所以两个正方形的面积之和不可能等于![]() .
.


科目:初中数学 来源: 题型:
【题目】圆O的半径为![]() ,点M的坐标为(m,3),若在圆O上存在一点N, 以M、N为正方形的两个顶点,且正方形的边均与两条坐标轴垂直,则m的最小值为_________
,点M的坐标为(m,3),若在圆O上存在一点N, 以M、N为正方形的两个顶点,且正方形的边均与两条坐标轴垂直,则m的最小值为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初二体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平况,进行了抽样调查,过程如下,请补充完整下题表格.
收集数据:从选择篮球和排球的学生各随机抽取10人,进行了测试,测试成绩如下:
排球9 9.5 9 9 8 10 9.5 8 4 9.5
篮球9.5 9.5 8.5 8.5 10 9.5 6 8 6 9
整理、描述数据:按如下分数段整理、描述这两组样本数据:
项目 人数 成绩x | 4.0≤x<5.5 | 5.5≤x<7.0 | 7.0≤x<8.5 | 8.5≤x<10 | 10 |
排球 | 1 | 0 | 2 | 6 | 1 |
篮球 | 0 | 2 | 1 | 6 | 1 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分折数据两组样本数据的平均数、中位数、众数如表所示:
项目 | 平均数 | 中位数 | 众数 |
排球 | 8.55 | a | 9和9.5 |
篮球 | 8.45 | 8.75 | b |
应用数据
(1)填空:a= ,b= .
p>(2)初三年级的小伟和小明看到上面数据后,小伟说:排球项目整体水平较高:小明说:篮球项目整体水平较高.你同意 的看法,理由为:① ;② .(从两个不同的角度说明推理的合理性)(3)如果初二年级有180人选排球项目,请信计该年级排球项目获得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
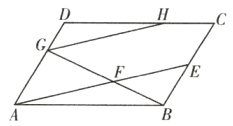
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一点,联结
上一点,联结![]() 并延长交边
并延长交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平分线,交射线
的平分线,交射线![]() 于点
于点![]() .设
.设![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)设![]() ,求关于
,求关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
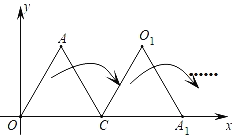
【题目】如图,已知点A在第一象限,点C的坐标为(1,0),△AOC是等边三角形,现把△AOC按如下规律进行旋转:第1次旋转,把△AOC绕点C按顺时针方向旋转120°后得到△A1O1C,点A1、O1分别是点A、O的对应点,第2次旋转,把△A1O1C绕着点A1按顺时针方向旋转120°后得到△A1O2C1,点O2、C1分别是点O1、C的对应点,第3次旋转,把△A1O2C1绕着点O2按顺时针方向旋转120°后得到△A2O2C2,点A2、C2分别是点A1、C1的对应点,……,依此规律,第6次旋转,把△A3O4C3绕着点O4按顺时针方向旋转120°后得到△A4O4C4,点A4、C4分别是点A3、C3的对应点,则点A4的坐标是( )
A.(![]() ,
,![]() )B.(6,0)C.(
)B.(6,0)C.(![]() ,
,![]() )D.(7,0)
)D.(7,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年九月是开学季,大多数学生会购买若干笔记本满足日常学习需要,校外某文具店老板开学前某日去批发市场进货,购进甲乙丙三种不同款式的笔记本共950本,已知甲款笔记本的进价为2元/本,乙款笔记本的进价是4元/本,丙款笔记本的进价是6元/本.
(1)本次进货共花费3300元,并且甲款的笔记本数量是乙款笔记本数量的2倍,请问本次购进丙款笔记本多少本?
(2)经过调研发现,甲款笔记本、乙款笔记本和丙款笔记本的零售价分别定为4元/本、6元/本和10元/本时,每天可分别售出甲款笔记本30本,乙款笔记本50本和丙款笔记本20本.如果将乙款笔记本的零售价提高![]() 元(a>25),甲款笔记本和丙款笔记本的零售价均保持不变,那么乙款笔记本每天的销售量将下降a%,丙款笔记本每天的销售量将上升
元(a>25),甲款笔记本和丙款笔记本的零售价均保持不变,那么乙款笔记本每天的销售量将下降a%,丙款笔记本每天的销售量将上升![]() a%,甲款笔记本每天的销量仍保持不变;若调价后每天销售三款笔记本共可获利260元,求a的值.
a%,甲款笔记本每天的销量仍保持不变;若调价后每天销售三款笔记本共可获利260元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
查看答案和解析>>
科目:初中数学 来源: 题型:
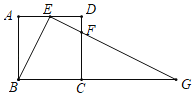
【题目】如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com