
分析 (1)根据题意把x=3,x=4代入,再比较其大小即可;
(2)假设x1<x2,且x1>0,x2>0,再作差比较即可.
解答 (1)解:∵f(x)=$\frac{1}{{x}^{2}}$(x>0),f(1)=$\frac{1}{{1}^{2}}$=1,f(2)=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$,
∴f(3)=$\frac{1}{{3}^{2}}$=$\frac{1}{9}$,f(4)=$\frac{1}{{4}^{2}}$=$\frac{1}{16}$,
∵$\frac{1}{9}$>$\frac{1}{16}$,
∴猜想f(x)=$\frac{1}{{x}^{2}}$(x>0)是减函数.
故答案为:$\frac{1}{9}$,$\frac{1}{16}$,减;
(2)证明:假设x1<x2,且x1>0,x2>0
f(x1)-f(x2)=$\frac{1}{{{x}_{1}}^{2}}$-$\frac{1}{{{x}_{2}}^{2}}$=$\frac{{x}_{2}^{2}-{x}_{1}^{2}}{{x}_{1}^{2}{x}_{2}^{2}}$=$\frac{{(x}_{2}-{x}_{1}{)(x}_{2}+{x}_{1})}{{x}_{1}^{2}{x}_{2}^{2}}$,
∵x1<x2,且x1>0,x2>0
∴x2-x1>0,x2+x1>0,x12•x22>0,
∴$\frac{{(x}_{2}-{x}_{1}){(x}_{2}+{x}_{1})}{{x}_{1}^{2}{x}_{2}^{2}}$>0,即f(x1)-f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)=$\frac{1}{{x}^{2}}$(x>0)是减函数.
点评 本题考查的是反比例函数综合题,根据题中所给出的材料假设出x1<x2,且x1>0,x2>0,再比较出其大小即可.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 没有交点 | B. | 只有一个交点,且它位于y轴右侧 | ||
| C. | 有两个交点,且它们均位于y轴左侧 | D. | 有两个交点,且它们均位于y轴右侧 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 93,96 | B. | 96,96 | C. | 96,100 | D. | 93,100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
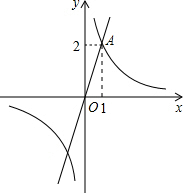 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com