
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的周长和面积.
【答案】
(1)
证明:∵DE∥OC,CE∥OD,
∵四边形OCED是平行四边形.
∴OC=DE,OD=CE
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴CE=OC=BO=DE.
∴四边形OCED是菱形
(2)
解:如图,连接OE.

在Rt△ADC中,AD=4,CD=3
由勾股定理得,AC=5∴OC=2.5
∴C菱形OCED=4OC=4×2.5=10,
在菱形OCED中,OE⊥CD,又∵OE⊥CD,
∴OE∥AD.
∵DE∥AC,OE∥AD,
∴四边形AOED是平行四边形,
∴OE=AD=4.
∴S菱形OCED= ![]() .
.
【解析】(1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,(2)根据S△ODC= ![]() S矩形ABCD以及四边形OCED的面积=2S△ODC即可解决问题.
S矩形ABCD以及四边形OCED的面积=2S△ODC即可解决问题.
【考点精析】根据题目的已知条件,利用矩形的性质的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个完全相同的标有数字1、2、3、4的小球. 小明从布袋里随机取出一个小球,记下数字为x,小红从布袋里剩下的小球中随机取出一个,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.
(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
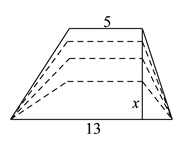
【题目】如图所示,梯形的上底长是![]() 厘米,下底长是
厘米,下底长是![]() 厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
(![]() )在这个变化过程中,自变量是__________,因变量是__________.
)在这个变化过程中,自变量是__________,因变量是__________.
(![]() )梯形的面积
)梯形的面积![]() 与高
与高![]() (厘米)之间的关系式为__________.
(厘米)之间的关系式为__________.
(![]() )当梯形的高由
)当梯形的高由![]() 厘米变化到
厘米变化到![]() 厘米时,梯形的面积由__________
厘米时,梯形的面积由__________![]() 变化到__________
变化到__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次歌手大赛中,10位评委对某歌手打分分别为:9.8,9.0,9.5,9.7,9.6,9.0,9.0,9.5,9.9,8.9,则去掉一个最高分一个最低分后,该歌手的得分应是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,则AK= .
,则AK= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个直棱柱,它有21条棱,其中一条侧棱长为20,底面各边长都为4.
(1)这是几棱柱?
(2)它有多少个面?多少个顶点?
(3)这个棱柱的所有侧面的面积之和是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com