
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角![]() 为
为![]() ,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角
,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角![]() 为
为![]() ,点A、B、C三点在同一水平线上.
,点A、B、C三点在同一水平线上.
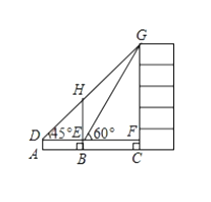
(1)求古树BH的高;
(2)求教学楼CG的高.
【答案】(1)8.5米;(2)![]() 米
米
【解析】
(1)利用等腰直角三角形的性质即可解决问题;
(2)作HJ⊥CG于G.则△HJG是等腰直角三角形,四边形EFJH是矩形,设GJ=EF=HJ=x.构建方程即可解决问题;
(1)由题意:四边形ABED是矩形,可得DE=AB=7米,AD=BE=1.5米,
在Rt△DEH中,∵∠HDE=45°,
∴HE=DE=7米,
∴BH=EH+BE=8.5米,
所以古树BH的高为8.5米;
(2)作HJ⊥CG于J.易证△HJG是等腰直角三角形,四边形EFJH是矩形,
∴JF=HE =7米,
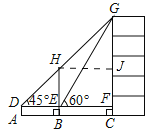
设HJ =x.则GJ=EF=HJ=x,
在Rt△EFG中,tan60°=![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (米);
(米);
所以教学楼CG的高为![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为![]() 个单位的正方形,在建立平面直角坐标系后,
个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.
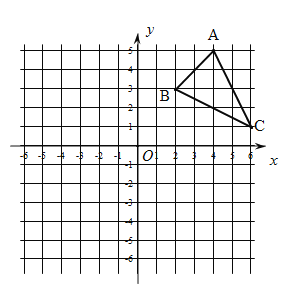
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)坐标平面的格点上确定一个点![]() ,使
,使![]() 是以
是以![]() 为底的等腰直角三角形,且点
为底的等腰直角三角形,且点![]() 在点
在点![]() 的下方,画出
的下方,画出![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:如图,∠ABC,射线BC上一点D.
求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等;

(2)在(1)的条件下,若∠ABC=60°,求等腰三角形△PBD顶角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是反比例函数![]() 与
与![]() 在x轴上方的图象,点C是y轴正半轴上的一点,过点C作
在x轴上方的图象,点C是y轴正半轴上的一点,过点C作![]() 轴分别交这两个图象与点A和点B,P和Q在x轴上,且四边形ABPQ为平行四边形,则四边形ABPQ的面积等于( )
轴分别交这两个图象与点A和点B,P和Q在x轴上,且四边形ABPQ为平行四边形,则四边形ABPQ的面积等于( )

A.20B.15C.10D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)
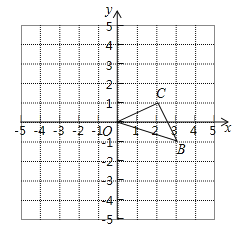
(1)以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),请在图中画出△B1 OC1,并写出这时B1的 坐标 ;
(2)将△BOC绕点O逆时针旋转90°后得到△B2OC2,请在图中作△B2OC2,,井写出这时点B2的坐标为 ;
(3)在(2)中的旋转过程中,求线段BC扫过的图形的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师为了了解班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查.他将调查结果分为四类:A:很好;B:较好;C:一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)请计算出A类男生和C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,张老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com