
ЁОЬтФПЁПШчЭМЂйЃЌШєжБЯпlЉUy=Ѓ2x+4НЛxжсгкЕуAЁЂНЛyжсгкЕуBЃЌНЋЁїAOBШЦЕуOФцЪБеыа§зЊ![]() ЕУЕНЁїCODЃЎЙ§ЕуAЃЌBЃЌDЕФХзЮяЯпhЉUy=ax2+bx+4ЃЎ
ЕУЕНЁїCODЃЎЙ§ЕуAЃЌBЃЌDЕФХзЮяЯпhЉUy=ax2+bx+4ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпhЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєгыyжсЦНааЕФжБЯпmвд1УыжгвЛИіЕЅЮЛГЄЕФЫйЖШДгyжсЯђзѓЦНвЦЃЌНЛЯпЖЮCDгкЕуMЁЂНЛХзЮяЯпhгкЕуNЃЌЧѓЯпЖЮMNЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЕуEЮЊХзЮяЯпhЕФЖЅЕуЃЌЕуPЪЧХзЮяЯпhдкЕкЖўЯѓЯоЕФЩЯвЛЖЏЕуЃЈВЛгыЕуDЁЂBжиКЯЃЉЃЌСЌНгPEЃЌвдPEЮЊБпзїЭМЪОвЛВрЕФе§ЗНаЮPEFGЃЎЫцзХЕуPЕФдЫЖЏЃЌе§ЗНаЮЕФДѓаЁЁЂЮЛжУвВЫцжЎИФБфЃЌЕБЖЅЕуFЛђGЧЁКУТфдкyжсЩЯЪБЃЌжБНгаДГіЖдгІЕФЕуPЕФзјБъЃЎ
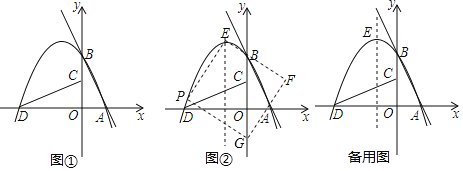
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШгЩжБЯпlЕФНтЮіЪНЕУЕНA,BСНЕуЕФзјБъЃЌдйИљОна§зЊЕУЕНDЕуЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпЕФНтЮіЪНМДПЩ.
ЃЈ2ЃЉЩшГіЕуNЕФзјБъЃЌзнзјБъгУКсзјБъБэЪОГіРДЃЌЭЌЪБвВПЩвдБэЪОГіMЕФзјБъЃЌЖјMNЕФГЄЖШОЭЪЧNЕугыMЕуЕФзнзјБъжЎВюЃЌзїВюжЎКѓЗЂЯжЪЧвЛИіЙигкNЕуКсзјБъЕФЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕМДПЩ.
ЃЈ3ЃЉЗжБ№ЖдЖЅЕуFКЭЖЅЕуGдкyжсЩЯЗжЧщПіЬжТлЃЌЧѓГіЕуPЕФзјБъМДПЩ
ЃЈ1ЃЉЁпжБЯпlЃК![]() НЛxжсгкЕуAЁЂНЛyжсгкЕуBЃЌ
НЛxжсгкЕуAЁЂНЛyжсгкЕуBЃЌ
Ёр![]() ЃЌ
ЃЌ![]() .
.
ЁпНЋ![]() ШЦЕуOФцЪБеыа§зЊ
ШЦЕуOФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() .
.
ЩшЙ§ЕуAЁЂBЁЂDЕФХзЮяЯпhЕФНтЮіЪНЮЊЃК![]() .
.
НЋBЕузјБъДњШыПЩЕУЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЙЪХзЮяЯпhЕФНтЮіЪНЮЊ
ЃЌЙЪХзЮяЯпhЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊ![]() .
.
ЩшNЕузјБъЮЊ![]() ЃЌдђMЕузјБъЮЊ
ЃЌдђMЕузјБъЮЊ![]() .
.
Ёр![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌMNзюДѓЃЌзюДѓжЕЮЊ
ЪБЃЌMNзюДѓЃЌзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєGЕудк yжсЩЯЃЌШчЭМЃЌзїPHЁЭyжсгкHЃЌНЛХзЮяЯпЖдГЦжсгкKЃЌ
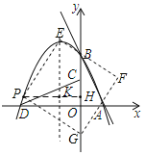
дк![]() КЭ
КЭ![]()
![]() жаЃЌ
жаЃЌ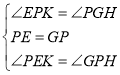 ЃЌ
ЃЌ ![]()
дђ![]() ЃЌ
ЃЌ![]() .
.
Ёп![]() ЃЌЁр
ЃЌЁр![]() .
.
Щш![]() ЃЌ
ЃЌ
дђЃК![]() ,
,![]() .
.
Ёр![]() ЃЌЫљвд
ЃЌЫљвд![]() .
.
вђДЫPЕуЕФзјБъЮЊЃК![]() ЃЌ
ЃЌ![]() .
.
ШєFЕудк yжсЩЯЃЌШчЭМЃЌзїPRДЙжБХзЮяЯпЖдГЦжсгкRЃЌFQДЙжБХзЮяЯпЖдГЦжсгкQЃЌдђ![]() PERЁе
PERЁе![]() EFQЃЌЁрER=FQЃЌ
EFQЃЌЁрER=FQЃЌ
ЫљвдЃЌ![]() ЃЌМДгаЃК
ЃЌМДгаЃК![]()
Ёр![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ

ЙЪPЕуЕФзјБъЮЊЃК![]() .
.
злЩЯЫљЪіЃЌТњзувЊЧѓЕФPЕуЕФзјБъгаШ§ИіЃЌЗжБ№ЮЊЃК
![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвEFЁЭABгкЕуCЃЌЕуDЪЧABбгГЄЯпЩЯвЛЕуЃЌЁЯAЃН30ЁуЃЌЁЯDЃН30ЁуЃЎ
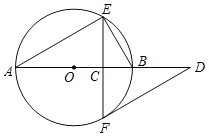
ЃЈ1ЃЉЧѓжЄЃКFDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШЁBEЕФжаЕуMЃЌСЌНгMFЃЌШєЁбOЕФАыОЖЮЊ2ЃЌЧѓMFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCЕФABБпЮЊдВOЕФЯвЃЌACЁЂBCЗжБ№НЛдВOгкDЁЂEЃЌЛЁAD=ЛЁBEЃЌЁЯC=60ЁуЃЛ

ЃЈ1ЃЉЧѓжЄЃКЁїABCЮЊЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌFЮЊЛЁADЩЯвЛЕуЃЌСЌНгFEВЂбгГЄжСGЃЌСЌНгBGЃЌШєЁЯAFB=ЁЯGЃЌЧѓЁЯFBGЕФе§ЯвжЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгFCВЂбгГЄНЛBGбгГЄЯпгкHЃЌШєCF=CHЃЌAF=7ЃЌHG=12ЃЌЧѓЯпЖЮBFЕФГЄЖШЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2+ЃЈ2m+1ЃЉx+mЃЈmЉ3ЃЉЃЌЃЈmЮЊГЃЪ§ЃЌЉ1ЁмmЁм4ЃЉЃЌAЃЈЉmЉ1ЃЌy1ЃЉЃЌ![]() ЪЧИУХзЮяЯпЩЯВЛЭЌЕФСНЕуЃЌЯжНЋХзЮяЯпЕФЖдГЦжсШЦзјБъдЕуOФцЪБеыа§зЊ90ЁуЕУЕНжБЯпaЃЌЙ§ХзЮяЯпЖЅЕуPзїPHЁЭaгкHЃЎ
ЪЧИУХзЮяЯпЩЯВЛЭЌЕФСНЕуЃЌЯжНЋХзЮяЯпЕФЖдГЦжсШЦзјБъдЕуOФцЪБеыа§зЊ90ЁуЕУЕНжБЯпaЃЌЙ§ХзЮяЯпЖЅЕуPзїPHЁЭaгкHЃЎ
ЃЈ1ЃЉЕБmЃН1ЪБЃЌЧѓГіетЬѕХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉШєЮоТлmШЁКЮжЕЃЌХзЮяЯпгыжБЯпyЃНxЉkmЃЈkЮЊГЃЪ§ЃЉгаЧвНігавЛИіЙЋЙВЕуЃЌЧѓkЕФжЕЃЛ
ЃЈ3ЃЉЕБ1ЃМPHЁм6ЪБЃЌЪдБШНЯy1ЃЌy2жЎМфЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌACЃНCBЃЌЕуEЃЌFЗжБ№ЪЧACЃЌBCЩЯЕФЕуЃЌЁїCEFЕФЭтНгдВНЛABгкЕуQЃЌDЃЎ
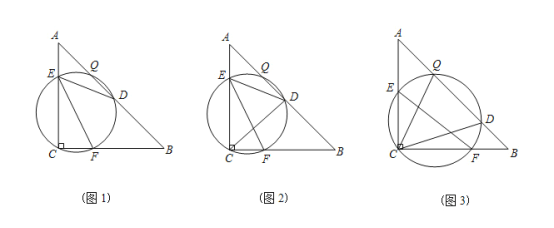
ЃЈ1ЃЉШчЭМ1ЃЌШєЕуDЮЊABЕФжаЕуЃЌЧѓжЄЃКЁЯDEFЃНЁЯBЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЮЪЕФЬѕМўЯТЃК
ЂйШчЭМ2ЃЌСЌНсCDЃЌНЛEFгкHЃЌACЃН4ЃЌШєЁїEHDЮЊЕШбќШ§НЧаЮЃЌЧѓCFЕФГЄЖШЃЎ
ЂкШчЭМ2ЃЌЁїAEDгыЁїECFЕФУцЛ§жЎБШЪЧ3ЃК4ЃЌЧвEDЃН3ЃЌЧѓЁїCEDгыЁїECFЕФУцЛ§жЎБШЃЈжБНгаДГіД№АИЃЉЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌСЌНгCQЃЌCDЃЌШєAE+BFЃНEFЃЌЧѓжЄЃКЁЯQCDЃН45ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгШ§НЧаЮЃЈВЛЪЧЕШбќШ§НЧаЮЃЉвЛИіЖЅЕув§ГівЛЬѕЩфЯпгыЖдБпЯрНЛЃЌЖЅЕугыНЛЕужЎМфЕФЯпЖЮАбетИіШ§НЧаЮЗжИюГЩСНИіаЁШ§НЧаЮЃЌШчЙћЗжЕУЕФСНИіаЁШ§НЧаЮжавЛИіЮЊЕШбќШ§НЧаЮЃЌСэвЛИігыдШ§НЧаЮЯрЫЦЃЌЮвУЧАбетЬѕЯпЖЮНазіетИіШ§НЧаЮЕФЭъУРЗжИюЯпЃЎ
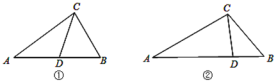
ЃЈ1ЃЉШчЭМЂйЃЌдкЁїABCжаЃЌCDЮЊНЧЦНЗжЯпЃЌЁЯA=40ЁуЃЌЁЯB=60ЁуЃЌЧѓжЄЃКCDЪЧЁїABCЕФЭъУРЗжИюЯпЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌдкЁїABCжаЃЌAC=2ЃЌBC=![]() ЃЌCDЪЧЁїABCЕФЭъУРЗжИюЯпЃЌЧвЁїACDЪЧвдCDЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЧѓЭъУРЗжИюЯпCDЕФГЄЃЎ
ЃЌCDЪЧЁїABCЕФЭъУРЗжИюЯпЃЌЧвЁїACDЪЧвдCDЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЧѓЭъУРЗжИюЯпCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯ:Шє![]() ЃЌЧѓmЁЂnЕФжЕ.
ЃЌЧѓmЁЂnЕФжЕ.
Нт: ![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() .
.
ИљОнФуЕФЙлВьЃЌЬНОПЯТУцЕФЮЪЬт:
ЃЈ1ЃЉМКжЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ЃЈ2ЃЉвбжЊЁїABCЕФШ§БпГЄaЁЂbЁЂcЖМЪЧе§ећЪ§ЃЌЧвТњзу![]() ЃЌЧѓБпcЕФзюДѓжЕ.
ЃЌЧѓБпcЕФзюДѓжЕ.
ЃЈ3ЃЉ ШєМКжЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() гы
гы![]() жсЕФвЛИіНЛЕуЮЊ
жсЕФвЛИіНЛЕуЮЊ![]() ЃЌгы
ЃЌгы![]() жсЕФИКАыжсНЛгкЕу
жсЕФИКАыжсНЛгкЕу![]() .
.
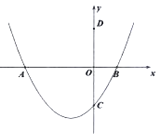
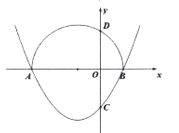
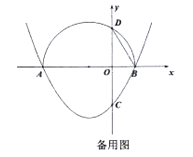
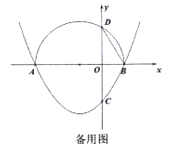
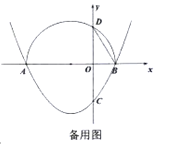
ЃЈ1ЃЉжБНгаДГіХзЮяЯпЕФЖдГЦжсЃЌМАХзЮяЯпгы![]() жсЕФСэвЛИіНЛЕу
жсЕФСэвЛИіНЛЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЕу![]() Йигк
Йигк![]() жсЕФЖдГЦЕуЮЊЕу
жсЕФЖдГЦЕуЮЊЕу![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дквд
дквд![]() ЮЊжБОЖЕФАыдВЩЯЪБЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЮЊжБОЖЕФАыдВЩЯЪБЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЬѕжЎжаЃЌЦфжавЛЬѕЪЧСэСНЬѕЫљМаНЧЕФНЧЦНЗжЯпЃПШєДцдкЃЌЧыЧѓГіЕу
Ш§ЬѕжЎжаЃЌЦфжавЛЬѕЪЧСэСНЬѕЫљМаНЧЕФНЧЦНЗжЯпЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯпЕФБэДяЪНЮЊ
жаЃЌХзЮяЯпЕФБэДяЪНЮЊ![]() ЃЌЯпЖЮABЕФСНИіЖЫЕуЗжБ№ЮЊAЃЈ1ЃЌ2ЃЉЃЌBЃЈ3ЃЌ2ЃЉ
ЃЌЯпЖЮABЕФСНИіЖЫЕуЗжБ№ЮЊAЃЈ1ЃЌ2ЃЉЃЌBЃЈ3ЃЌ2ЃЉ
ЃЈ1ЃЉШєХзЮяЯпОЙ§дЕуЃЌЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЖЅЕуCЕФзјБъЃЈгУКЌгаmЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉШєХзЮяЯпгыЯпЖЮABЧЁгавЛИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓГіmЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com