
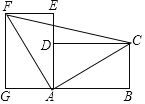
【题目】如图,将两块完全相同的矩形纸片ABCD和矩形纸片AEFG按图示方式放置(点A、D、E在同一直线上),连接AC、AF、CF,已知AD=3,DC=4,则CF的长是( )
A.5B.7C.5![]() D.10
D.10
【答案】C
【解析】
由两块完全相同的矩形纸片ABCD和矩形纸片AEFG,得出AG=AD=BC=3,FG=AB=CD=4,∠FGA=∠ABC=90°,由勾股定理求出AC=5,由SAS证得△FGA≌△ABC,得出AF=AC,∠GFA=∠BAC,∠GAF=∠BCA,由∠GFA+∠GAF=90°,推出∠GAF+BAC=90°,得出∠FAC=90°,即△CAF是等腰直角三角形,即可得出结果.
∵两块完全相同的矩形纸片ABCD和矩形纸片AEFG,
∴AG=AD=BC=3,FG=AB=CD=4,∠FGA=∠ABC=90°,
AC=![]() =5,
=5,
在△FGA和△ABC中,
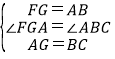 ,
,
∴△FGA≌△ABC(SAS),
∴AF=AC,∠GFA=∠BAC,∠GAF=∠BCA,
∵∠GFA+∠GAF=90°,
∴∠GAF+BAC=90°,
∴∠FAC=90°,
∴△CAF是等腰直角三角形,
∴CF=![]() AC=5
AC=5![]() ,
,
故选C.


科目:初中数学 来源: 题型:
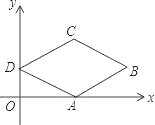
【题目】如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )
A. 8B. 16C. 24D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,点P从点A向点D运动,点Q从点C向点B运动.已知点P的运动速度为1cm/s,点Q的运动速度为2cm/s,AD=4cm,BC=8cm,运动时间为t.当t=_____S时,四边形ABQP是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=![]() ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会与实践的课堂上,刘老师组织七(1)班的全体学生用硬纸板制作圆柱体(图1).七(1)班共有学生50人,其中男生人数比女生人数少2人,并且每名学生每小时剪20个圆柱侧面(图2)或剪10个圆柱底面(图3).
(1)七(1)班有男生、女生各多少人?
(2)原计划男生负责剪圆柱侧面,女生负责剪圆柱底面,要求一个圆柱侧面配两个圆柱底面,那么每小时剪出的筒身与筒底能配套吗?如果不配套,那么男生应向女生支援多少人时,才能使每小时内剪出的侧面与底面配套.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣![]() x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
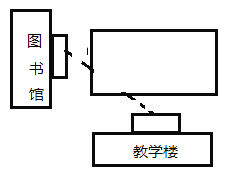
【题目】如图某学校从教学楼到图书馆总有少数同学不走人行道,而横穿草坪.
(1)试用所学的知识来说明少数学生这样走的理由;
(2)请问学生这样走行吗?如不行请你在草坪上竖起一个牌子,写上一句话来警示学生应该怎样做.
查看答案和解析>>
科目:初中数学 来源: 题型:
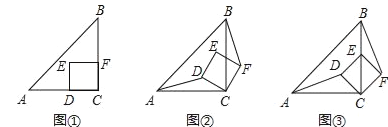
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D、F分别在边AC、BC上,易证:AD=BF(不需要证明);
探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD、BF,其他条件不变,如图②,求证:AD=BF;
应用:若α=45°,CD=![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
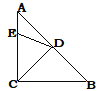
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com