
科目:初中数学 来源: 题型:解答题
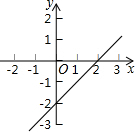 如图所示,是函数y=kx+b的图象,利用图象解答:
如图所示,是函数y=kx+b的图象,利用图象解答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30秒 | B. | 40秒 | C. | 50秒 | D. | 60秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )
小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )| A. | 4 | B. | 5 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解一批汽车轮胎的使用年限,应采用抽样调查的方式 | |
| B. | “50名同学中恰有2名同学的生日是同一天”属于随机事件 | |
| C. | “早晨的太阳从东方升起”属于必然事件 | |
| D. | “长为3cm,5cm,9cm的三条线段围成一个三角形”属于可能事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
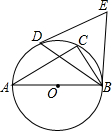 如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )
如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等边三角形 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com