

分析 (1)设CH=GH=DG=x,根据DC=DH+CH=1,列出方程即可求出HC,然后运用三角函数的定义求出tan∠HBC的值.
(2)只需借鉴阅读中证明“四边形BCEF为$\sqrt{2}$矩形”的方法就可解决问题.
(3)利用(2)中结论,寻找规律可得到n的值.
解答 解:(1)如图①中,由折叠可得:
DG=HG,GH=CH,
∴DG=GH=CH.
设HC=x,则DG=GH=x.
∵∠DGH=90°,
∴DH=$\sqrt{2}$x,
∴DC=DH+CH=$\sqrt{2}$x+x=1,
解得x=$\sqrt{2}$-1.
∴tan∠HBC=$\frac{HC}{BC}$=$\frac{\sqrt{2}-1}{1}$=$\sqrt{2}$-1.
故答案为:GH、DG,$\sqrt{2}-1$;
(2)如图②中,∵BC=1,EC=BF=$\frac{\sqrt{2}}{2}$,
∴BE=$\sqrt{E{C}^{2}+B{C}^{2}}$=$\frac{\sqrt{6}}{2}$
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,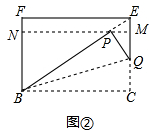
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴$\frac{BP}{BE}$=$\frac{BN}{BF}$,
即BP•BF=BE•BN,
∴1×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$BN,
∴BN=$\frac{\sqrt{3}}{3}$,
∴BC:BN=1:$\frac{\sqrt{3}}{3}$=$\sqrt{3}$:1,
∴四边形BCMN是$\sqrt{3}$的矩形;
(3)同理可得:
将$\sqrt{3}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{4}$矩形”,
将$\sqrt{4}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{5}$矩形”,
将$\sqrt{5}$矩形沿用(2)中的方式操作1次后,得到一个“$\sqrt{6}$矩形”,
所以将图②中的$\sqrt{3}$矩形BCMN沿用(2)中的方式操作3次后,得到一个“$\sqrt{6}$矩形”.
故答案为6.
点评 本题主要考查了轴对称的性质、正方形的性质、矩形的判定与性质、平行线分线段成比例、勾股定理等知识,考查了阅读理解能力、操作能力、归纳探究能力、推理能力,运用已有经验解决问题的能力,是中考创新题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
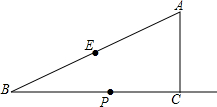 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
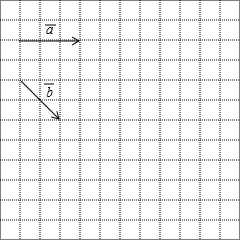 如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).
如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
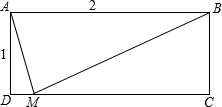 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{4}$ | C. | $\sqrt{3}-\frac{3}{2}$ | D. | $2-\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com