
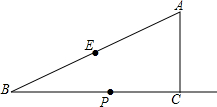
 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$. 分析 根据30°角所对的直角边等于斜边的一半可求出AB,即可得到AE的值,然后根据勾股定理求出BC.①若PA′与AB交于点F,连接A′B,如图1,易得S△EFP=$\frac{1}{2}$S△BEP=$\frac{1}{2}$S△A′EP,即可得到EF=$\frac{1}{2}$BE=BF,PF=$\frac{1}{2}$A′P=A′F.从而可得四边形A′EPB是平行四边形,即可得到BP=A′E,从而可求出BP;②若EA′与BC交于点G,连接AA′,交EP与H,如图2,同理可得GP=BG,EG=$\frac{1}{2}$EA′=1,根据三角形中位线定理可得AP=2=AC,此时点P与点C重合(BP=BC),从而可求出BP.
解答 解:∵∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,
∴AB=4,AE=$\frac{1}{2}$AB=2,BC=2$\sqrt{3}$.
①若PA′与AB交于点F,连接A′B,如图1.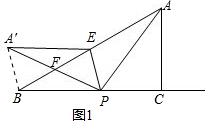
由折叠可得S△A′EP=S△AEP,A′E=AE=2,.
∵点E是AB的中点,
∴S△BEP=S△AEP=$\frac{1}{2}$S△ABP.
由题可得S△EFP=$\frac{1}{4}$S△ABP,
∴S△EFP=$\frac{1}{2}$S△BEP=$\frac{1}{2}$S△AEP=$\frac{1}{2}$S△A′EP,
∴EF=$\frac{1}{2}$BE=BF,PF=$\frac{1}{2}$A′P=A′F.
∴四边形A′EPB是平行四边形,
∴BP=A′E=2;
②若EA′与BC交于点G,连接AA′,交EP与H,如图2.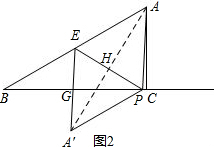 .
.
同理可得GP=$\frac{1}{2}$BP=BG,EG=$\frac{1}{2}$EA′=$\frac{1}{2}$×2=1.
∵BE=AE,∴EG=$\frac{1}{2}$AP=1,
∴AP=2=AC,
∴点P与点C重合,
∴BP=BC=2$\sqrt{3}$.
故答案为2或2$\sqrt{3}$.
点评 本题主要考查了轴对称的性质、30°角所对的直角边等于斜边的一半、勾股定理、平行四边形的判定与性质、等高三角形的面积比等于底的比、三角形中位线定理等知识,运用分类讨论的思想是解决本题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
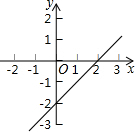 如图所示,是函数y=kx+b的图象,利用图象解答:
如图所示,是函数y=kx+b的图象,利用图象解答:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
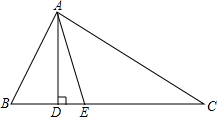 如图,△ABC中,AD⊥BC于D,AE平分∠BAC交BC边于点E,∠C=2∠DAE,AC=11,AB=6,则CE=$\frac{55}{6}$.
如图,△ABC中,AD⊥BC于D,AE平分∠BAC交BC边于点E,∠C=2∠DAE,AC=11,AB=6,则CE=$\frac{55}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解一批汽车轮胎的使用年限,应采用抽样调查的方式 | |
| B. | “50名同学中恰有2名同学的生日是同一天”属于随机事件 | |
| C. | “早晨的太阳从东方升起”属于必然事件 | |
| D. | “长为3cm,5cm,9cm的三条线段围成一个三角形”属于可能事件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com