
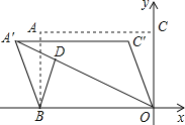
【题目】如图,在平面直角坐标系中,矩形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,AC长为![]() ,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=
,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=![]() 的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
【答案】-![]() .
.
【解析】
当BD⊥OA′时,BD取得最小值,延长A′C′交y轴于E,易得△BDO∽△OEA′,结合A'坐标为(-4,2),得![]() =
=![]() =
=![]() ,从而得BD=1,OD=2,作DF⊥OB于F,得DF=
,从而得BD=1,OD=2,作DF⊥OB于F,得DF=![]() ,进而得到点D的坐标,即可求解.
,进而得到点D的坐标,即可求解.
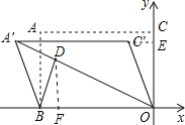
当BD⊥OA′时,BD取得最小值,
延长A′C′交y轴于E,如图,
∵A′C′∥OB,
∴A′E⊥y轴,∠BOD=∠EA′O,
∴∠BDO=∠OEA′,
∴△BDO∽△OEA′,
∴![]() =
=![]() =
=![]() ,
,
∵A'坐标为(-4,2),
∴A′E=4,OE=2,
∴OA′=![]() =2
=2![]() ,
,
∵OB=AC=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴BD=1,OD=2,
作DF⊥OB于F,
∵![]() BDOD=
BDOD=![]() OBDF,即1×2=
OBDF,即1×2=![]() DF,
DF,
∴DF=![]() ,
,
∴D的纵坐标为![]() ,
,
设直线OA′的解析式为y=kx,
∴2=-4k,解得k=-![]() ,
,
∴直线OA′的解析式为y=-![]() x,
x,
把y=![]() 代入得,
代入得,![]() =-
=-![]() x,解得x=-
x,解得x=-![]() ,
,
∴D(-![]() ,
,![]() ),
),
∵反比例函数y=![]() 的图象过D点,
的图象过D点,
∴k=-![]() ×
×![]() =-
=-![]() ,
,
故答案为:-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度向终点
出发,以每秒3个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 边或
边或![]() 边于点
边于点![]() ,点
,点![]() 是射线
是射线![]() 边上一点,总保持
边上一点,总保持![]() ,以
,以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
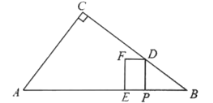
(1)用含![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒5个单位长度的速度沿
上以每秒5个单位长度的速度沿![]() 往返一次,连结
往返一次,连结![]() 、
、![]() ,直接写出矩形
,直接写出矩形![]() 的面积是
的面积是![]() 的面积的2倍时
的面积的2倍时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童用药的剂量常常按他们的体重来计算,某种药品,体重![]() 的儿童,每次正常服用量为
的儿童,每次正常服用量为![]() ;体重
;体重![]() 的儿童每次正常服用量为
的儿童每次正常服用量为![]() ;体重在
;体重在![]() 范围内时,每次正常服用量
范围内时,每次正常服用量![]() 是儿童体重
是儿童体重![]() 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若该药品的一种包装规格为![]() /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
/袋,求体重在什么范围的儿童生病时可以一次服下一袋药?
查看答案和解析>>
科目:初中数学 来源: 题型:
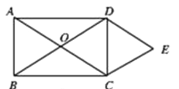
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果按照果径大小可分为4个等级:标准果、优质果、精品果、礼品果,某采购商从采购的一批该种水果中随机抽取100个,利用它的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,售价为20元/个;
方案2:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/个) | 16 | 18 | 22 | 24 |
(1)从采购商的角度考虑,应该采用哪种购销方案?
(2)若采购商采购的该种水果的进价不超过20元/个,则采购商可以获利,现从这种水果的4个等级中任选2种,按方案2进行购买,求这2种等级的水果至少有一种能使采购商获利的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
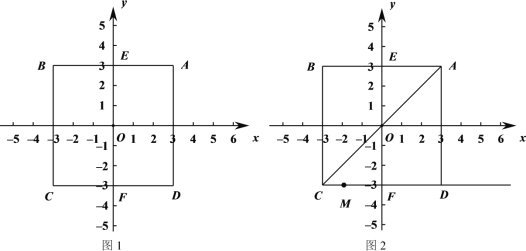
【题目】对于平面直角坐标系xOy中的点P和图形N,给出如下定义:如果Q为图形N上一个动点,P,Q两点间距离的最大值为dmax,P,Q两点间距离的最小值为dmin,我们把dmax + dmin的值叫点P和图形N间的“和距离”,记作d(P,图形N).
(1)如图,正方形ABCD的中心为点O,A(3,3).
① 点O到线段AB的“和距离”d(O,线段AB)= ;
② 设该正方形与y轴交于点E和F,点P在线段EF上,d(P,正方形ABCD)=7,求点P的坐标.
(2)如图2,在(1)的条件下,过C,D两点作射线CD,连接AC,点M是射线CD上的一点,如果![]() d(M,线段AD)
d(M,线段AD)![]() ,直接写出M点横坐标t取值范围.
,直接写出M点横坐标t取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
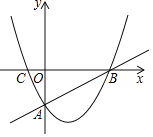
【题目】如图,直线y=![]() x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣
x﹣2与x轴交于点B,与y轴交于点A,抛物线y=ax2﹣![]() x+c经过A,B两点,与x轴的另一交点为C.
x+c经过A,B两点,与x轴的另一交点为C.
(1)求抛物线的解析式;
(2)M为抛物线上一点,直线AM与x轴交于点N,当![]() 时,求点M的坐标;
时,求点M的坐标;
(3)P为抛物线上的动点,连接AP,当∠PAB与△AOB的一个内角相等时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过⊙T(半径为r)外一点P引它的一条切线,切点为Q,若0<PQ≤2r,则称点P为⊙T的伴随点.
(1)当⊙O的半径为1时,
①在点A(4,0),B(0,![]() ),C(1,
),C(1,![]() )中,⊙O的伴随点是 ;
)中,⊙O的伴随点是 ;
②点D在直线y=x+3上,且点D是⊙O的伴随点,求点D的横坐标d的取值范围;
(2)⊙M的圆心为M(m,0),半径为2,直线y=2x﹣2与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙M的伴随点,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com