
����Ŀ�������ļ������٣�����ҹ�д�Ϻ�г��𱬣���Ϻ����Ӧ��Ϻ��ֳ��ĪС��Ϊ���չ˸���Ŀͻ��ƶ����������۷�������������������50��IJ��֣�46Ԫ/�������������50�ﵫ������m��120��m��200����IJ��֣�60Ԫ/�������������m��IJ��֣�80Ԫ/�
��1������������ĪС�������ô�Ϻ80�����Ӧ������ԪǮ��
��2������������ĪС�������ô�Ϻx�Ӧ����Ǯ��ΪyԪ�����г�y����x�ĺ�������ʽ��
��3������������ĪС�������ô�Ϻ160�Ӧ��Ǯ��yԪ��ȡֵ��Χ��8000��y��9000������m��ȡֵ��Χ��
���𰸡���1����Ӧ��4100Ԫ����2��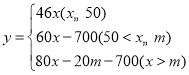 ����3��155��m��160��
����3��155��m��160��
��������
��1������������ʽ���㣻
��2���������������x��50ʱ����50��x��m��120��m��200��ʱ����x��mʱ���ֱ��г���������µĺ�������ʽ���ɣ�
��3����x��160ʱ���ɣ�2��֪������������ۣ���120��m��160ʱ�͵�m��160ʱ���г�����m�IJ���ʽ�飬��֮���ɣ�
�⣺��1��������֪��
����������ĪС�������ô�Ϻ80�����Ӧ����Ǯ��Ϊ��50��46+��80��50����60��4100��Ԫ��
������������ĪС�������ô�Ϻ80�����Ӧ��4100ԪǮ��
��2����x��50ʱ��y��46x��
��50��x��m��120��m��200��ʱ��y��50��46+��x��50����60��60x��700��
��x��mʱ��y��50��46+��m��50����60+��x��m����80��80x��20m��700��
��y����x�ĺ�������ʽΪ��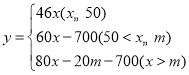 ��
��
��3����x��160ʱ���ɣ�2��֪������������ۣ�
�ٵ�120��m��160ʱ��y��80x��20m��700
��8000��80��160��20m��700��9000
��ã�155��m��205
��155��m��160��
�ڵ�m��160ʱ��y��60x��700����ʱ60��160��700��9530��9000��������8000��y��9000������m��160��������
����������155��m��160��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ8����E�ڱ�AD�ϣ���F��CD�ϣ�DF��![]() ��tan��DEF��
��tan��DEF��![]() ��
��
��1����AE�ij���
��2����֤��BE��EF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
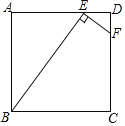
����Ŀ������ѧ����ϣ���ʦ�����һ�����⣺��һ�����dz���ͼ�ڷţ�ֱ�����dzߵ�����ֱ�DZ߷ֱ�ֱ��ƽ�У�60���ǵĶ�������һ�����dzߵ�б�����ƶ���������˶������У�����Щ���������о�����֮��Ĺ�ϵ��
С��ѡ��������һ�Ա���������ѧϰ�����ľ��飬������֮��Ĺ�ϵ������̽����
������С�ֵ�̽�����̣��벹��������
��1����������ͼ�Σ���ȷ������̽������
��ͼ2����Rt��ABC�У���C=90����AC=BC=6cm��D���߶�AB��һ���㣬����DE��BC�ڵ�E����EDF=60��������DF������AC���ڵ�F����B��E�����ľ���Ϊxcm��E��F�����ľ���Ϊycm��
��2��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
��˵������ȫ����ʱ������ݱ���һλС����
��3������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��4����ϻ����ĺ���ͼ������⣺����DEFΪ�ȱ�������ʱ��BE�ij���ԼΪ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ�����l1��l2����ƽ�У�A��B��l1�ϵ����㣬C��D��l2�ϵ����㣬ijͬѧ��A����á�CAB��90������DAB��30��������AB������20�����E����AE��20������á�DEB��60��.��C��D�����ľ���.
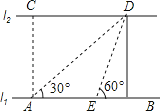
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1��¥��2��¥���ϲ࣬¥���ΪAB�����������磬̫��������ˮƽ�����ɵĽ�Ϊ32.3����1��¥��2��¥ǽ���ϵ�Ӱ��ΪCA�����������磬̫��������ˮƽ�����ɵĽ�Ϊ55.7����1��¥��2��¥ǽ���ϵ�Ӱ��ΪDA����֪CD=35m���������¥֮��ľ���AB�ij��ȣ��������������
���ο����ݣ�sin32.3���0.53��cos32.3���0.85��tan32.3���0.63��sin55.7���0.83��cos55.7���0.56��tan55.7���1.47��
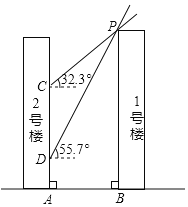
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�DZ߳�Ϊ4�ĵȱ������Σ���AB������OM�ϣ���OA��6����D������OM�ϵĶ��㣬����D�����A�غ�ʱ������ACD�Ƶ�C��ʱ�뷽����ת60���õ���BCE������DE��
��1����ͼ1����֤����CDE�ǵȱ������Σ�
��2����OD��t��
�ٵ�6��t��10ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE�ܳ�����Сֵ���������ڣ���˵�����ɣ�
����tΪ��ֵʱ����DEB��ֱ�������Σ�ֱ��д��������ɣ���
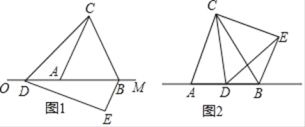
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y��ax2��2ax��3a��a��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y��������ύ�ڵ�C������ΪD��
��1����D�����꣨�ú�a�Ĵ���ʽ��ʾ����
��2������ADΪֱ����Բ������C��
���������ߵĺ�����ϵʽ��
����ͼ2����E��y�Ḻ������һ�㣬����BE������OBE��ƽ����ijһ����ת180�㣬�õ���PMN����P��M��N�ֱ�͵�O��B��E��Ӧ�������ҵ�M��N�����������ϣ���MF��x���ڵ�F�����߶�MF��BF��1��2�����M��N�����ꣻ
�۵�Q�������ߵĶԳ����ϣ���QΪԲ�ĵ�Բ��A��B���㣬���Һ�ֱ��CD���У���ͼ3�����Q�����꣮
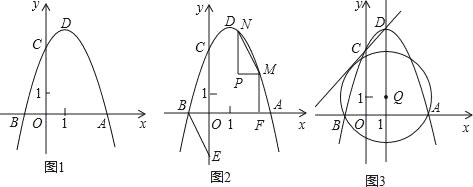
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
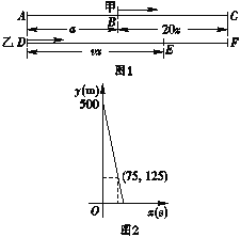
����Ŀ����ͼ1��ʾ���ס���������ֱ·ͬ����ʻ�����ٷֱ�Ϊ20 m/s��v(m/s)������׳����� ��ǰa (m)��������ͬʱ���������ҳ��ϼ׳�ʱ��������ֹͣ��ʻ����x(s)���������y (m)��y��x�ĺ�����ϵ��ͼ2��ʾ�������½��ۣ�
��ͼ1��a��ֵΪ500��
���ҳ����ٶ�Ϊ35 m/s��
��ͼ1���߶�EFӦ��ʾΪ![]() ��
��
��ͼ2�к���ͼ����x�ύ��ĺ�����Ϊ100��
�������е���ȷ�������� ��
A. �٢� B. �ڢ�
C. �٢ڢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������Լ�ò�����ͬһ·��ͬһ������ij���㼯�ϣ���֪���Ҷ������660�ף�����ͬʱ����������24����ʱ�������Ҿ��뾰������ȵ���Ⱥ�ף�������30����Ҳ�����˾�����������.���������߹����У��ס������˾����ָ��Ե��ٶ��������ߣ��ס�����������·��![]() ���ף���׳�����ʱ��
���ף���׳�����ʱ��![]() �����ӣ�֮��Ĺ�ϵ��ͼ��ʾ������˵��������ǣ� ��
�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ������˵��������ǣ� ��

A.���ٶ���70��/��B.�ҵ��ٶ���60��/��
C.���뾰��2100��D.�Ҿ��뾰��420��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com