
【题目】如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=![]() (x>0)的图象上,延长CA交y轴于点D,AD=1.
(x>0)的图象上,延长CA交y轴于点D,AD=1.
(1)求该反比例函数的解析式;
(2)将△ABC绕点B顺时针旋转得到△EBF,使点C落在x轴上的点F处,点A的对应点为E,求旋转角的度数和点E的坐标.

【答案】(1) y=![]() ;(2) 旋转角为120°, E点坐标为(2+
;(2) 旋转角为120°, E点坐标为(2+![]() ,
,![]() )
)
【解析】
(1)设A(1,k),再表示出B(3,k-4),则利用反比例函数图象上点的坐标特征得到3(k-4)=k,解方程求出k即可得到该反比例函数的解析式;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,根据旋转的性质得BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,再计算出BM=CM-BC=2,则在Rt△BMF中,利用三角函数可求出∠MBF=60°,MF=![]() ,BM=
,BM=![]() ,于是得到旋转角为120°,然后证明Rt△BMF∽Rt△FNE,利用相似比求出FN和EN,从而可得到E点坐标.
,于是得到旋转角为120°,然后证明Rt△BMF∽Rt△FNE,利用相似比求出FN和EN,从而可得到E点坐标.
解:(1)∵AC∥x轴,AD=1,
∴A(1,k),
∵∠C=90°,AC=2,BC=4,
∴B(3,k﹣4),
∵点B在y=![]() 的图象上,
的图象上,
∴3(k﹣4)=k,解得k=6,
∴该反比例函数的解析式为y=![]() ;
;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,
∵△ABC绕点B顺时针旋转得到△EBF,
∴BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,
∵BC⊥x轴,A(1,6),
∴BM=CM﹣BC=6﹣4=2,
在Rt△BMF中,∵cos∠MBF=![]() =
=![]() =
=![]() ,
,
∴∠MBF=60°,MF=![]() BM=
BM=![]() ,
,
∴∠CBF=180°﹣∠MBF=120°,
∴旋转角为120°;
∵∠BFM+∠MBF=90°,∠BFM+∠EFN=90°,
∴∠MBF=∠EFN,
∴Rt△BMF∽Rt△FNE,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴FN=1,EN=![]() ,
,
∴ON=OM+MF+FN=1+![]() +1=2+
+1=2+![]() ,
,
∴E点坐标为(2+![]() ,
,![]() ).
).


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,O为坐标原点,点A(3,4),点B(6,0).
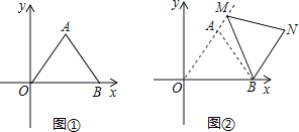
(1)如图①,求AB的长;
(2)如图2,把图①中的△ABO绕点B顺时针旋转,使O的对应点M恰好落在OA的延长线上,N是点A旋转后的对应点;
①求证:四边形AOBN是平行四边形;
②求点N的坐标.
(3)点C是OB的中点,点D为线段OA上的动点,在△ABO绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长方形镜面玻璃的四周,镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是3:1.已知镜面玻璃的价格是每平方米100元,边框的价格是每米20元,另外制作这面镜子还需加工费55元.如果制作这面镜子共花了210元,求这面镜子的长是__________![]() ,宽是___________
,宽是___________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
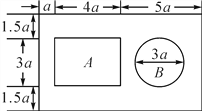
【题目】某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.(π取3.14)
(1)活动场所和花草的面积各是多少?
(2)整座健身馆的面积是成年人活动场所面积的多少倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
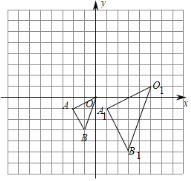
【题目】在如图所示的方格中,△OAB 的顶点坐标分别为 O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1 与△OAB 是以点 P 为位似中心的位似图形.
(1)位似中心 P 的坐标是 ,△O1A1B1与△OAB 的相似比为 ;
(2)以原点 O 为位似中心,在 y 轴的左侧画出△OAB 的另一个位似三角形![]() ,使它与△OAB 的相似比为 2:1,并写出点 B 的对应点
,使它与△OAB 的相似比为 2:1,并写出点 B 的对应点![]() 的坐标是 .
的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
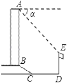
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,则大楼AB的高度为________米.
,则大楼AB的高度为________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com