
����Ŀ����ͼ1����ֱ֪��y=kx��������y= ![]() ���ڵ�A��3��6����
���ڵ�A��3��6����
��1����ֱ��y=kx�Ľ���ʽ���߶�OA�ij��ȣ�
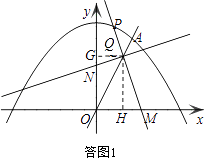
��2����PΪ�����ߵ�һ�����ڵĶ��㣬����P��ֱ��PM����x���ڵ�M����M��O���غϣ�����ֱ��OA�ڵ�Q���ٹ���Q��ֱ��PM�Ĵ��ߣ���y���ڵ�N����̽�����߶�QM���߶�QN�ij���֮���Ƿ�Ϊ��ֵ������ǣ���������ֵ��������ǣ�˵�����ɣ�
��3����ͼ2������BΪ�������϶Գ����Ҳ�ĵ㣬��E���߶�OA�ϣ����O��A���غϣ�����D��m��0����x���������ϵĶ��㣬�������BAE=��BED=��AOD������̽����m��ʲô��Χʱ������������E��ĸ����ֱ���1����2����
���𰸡�
��1��
�⣺�ѵ�A��3��6������y=kx �ã�
��6=3k��
��k=2��
��y=2x��
OA= ![]()
��2��
�⣺����һ��
![]() ��һ����ֵ���������£�
��һ����ֵ���������£�
���ͼ1������Q��QG��y���ڵ�G��QH��x���ڵ�H��
�ٵ�QH��QM�غ�ʱ����ȻQG��QN�غϣ�
��ʱ ![]() =tan��AOM=2��
=tan��AOM=2��
�ڵ�QH��QM���غ�ʱ��
��QN��QM��QG��QH
�������H��G�ֱ���x��y����������ϣ�
���MQH=��GQN��
�֡ߡ�QHM=��QGN=90��
���QHM�ס�QGN����
�� ![]() =tan��AOM=2��
=tan��AOM=2��
����P��Q�������ߺ�ֱ���ϲ�ͬλ��ʱ��ͬ���ɵ� ![]() =2
=2
��������
����Q�ֱ���y�ᣬx�ᴹ�ߣ�����ֱ�ΪG��H��
��QN��QM�����NQH+��HQM=90�㣬
��QG��QH�����NQH+��GQN=90�㣬
���HQM=��GQN��
�ߡ�QGN=��QHM=90�㣬
���QGN�ס�QHM��
��QM��QN=2��1
��3��
�⣺����һ�����ͼ2��
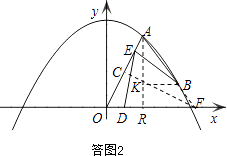
�ӳ�AB��x���ڵ�F������F��FC��OA�ڵ�C������A��AR��x���ڵ�R
�ߡ�AOD=��BAE��
��AF=OF��
��OC=AC= ![]() OA=
OA= ![]()
�ߡ�ARO=��FCO=90�㣬��AOR=��FOC��
���AOR�ס�FOC��
�� ![]() ��
��
��OF= ![]() ��
��
���F�� ![]() ��0����
��0����
���B��x���� ![]() ����
����
����B��BK��AR�ڵ�K�����AKB�ס�ARF��
�� ![]() ��
��
�� ![]() ��
��
���x1=6��x2=3����ȥ����
���B��6��2����
��BK=6��3=3��AK=6��2=4��
��AB=5��
����ABҲ�ɲ�������ķ�����
��ֱ��AFΪy=kx+b��k��0���ѵ�A��3��6������F�� ![]() ��0�������
��0�������
k=�� ![]() ��b=10��
��b=10��
��y=�� ![]() x+10��
x+10��
�� 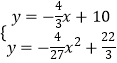 ��
��
�� ![]() ����ȥ����
����ȥ���� ![]() ��
��
��B��6��2����
��AB=5
�������������AB�ij�������֣�
�ڡ�ABE���OED��
�ߡ�BAE=��BED��
���ABE+��AEB=��DEO+��AEB��
���ABE=��DEO��
�ߡ�BAE=��EOD��
���ABE�ס�OED��
��OE=a����AE=3 ![]() ��a��0��a��3
��a��0��a��3 ![]() ����
����
�ɡ�ABE�ס�OED�� ![]() ��
��
�� ![]() =
= ![]() ��
��
��m= ![]() a��3
a��3 ![]() ��a��=��
��a��=�� ![]() a2+
a2+ ![]() a��0��a��3
a��0��a��3 ![]() ����
����
�ඥ��Ϊ�� ![]() ��
�� ![]() ��
��
���ͼ3��
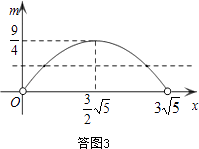
��m= ![]() ʱ��OE=a=
ʱ��OE=a= ![]() ����ʱE����1����
����ʱE����1����
��0��m�� ![]() ʱ����ȡһ��m��ֵ����Ӧ������aֵ����ʱE����2����
ʱ����ȡһ��m��ֵ����Ӧ������aֵ����ʱE����2����
�൱m= ![]() ʱ��E��ֻ��1��
ʱ��E��ֻ��1��
��0��m�� ![]() ʱ��E����2��
ʱ��E����2��
��������
�ӳ�AB��x����F������F��FC��OA�ڵ�C��
�ߡ�BAE=��AOD��
��OF=AF��
��FC��OA��
��CΪOA�е㣬
��O��0��0����A��3��6����
��C�� ![]() ��3����
��3����
KOA=2��
��KOA��KPC=��1��
��KPC=�� ![]() ��
��
��lFC��y=�� ![]() x+
x+ ![]() ��
��
��y=0ʱ��x= ![]() ����F��
����F�� ![]() ��0����
��0����
��lAF��y=�� ![]() x+10��
x+10��
�� 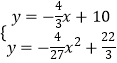 x1=3���ᣩ��x2=6��
x1=3���ᣩ��x2=6��
��B��6��2����AB=5��
��D��m��0����OD=m��
��AE=a��OE=3 ![]() ��a��
��a��
 ��OED=��ABE��
��OED=��ABE��
���ABE�ס�OED��
�� ![]() ��
��
�� ![]() ��
��
��a2�� ![]() a+5m=0��
a+5m=0��
��Eֻ��һ����
���=45��20m=0��
��m= ![]() ��
��
��Eֻ��������
���=45��20m��0��
��0��m�� ![]() ʱ��E������
ʱ��E������
����������1�����ô���ϵ�������ֱ��y=kx�Ľ���ʽ������A�������ù��ɶ�������߶�OA�ij��ȣ���2�����ͼ1������Q��QG��y���ڵ�G��QH��x���ڵ�H���������������Ρ�QHM���QGN�����߶�QM���߶�QN�ij���֮��ת��Ϊ���������ε����Ʊȣ��� ![]() =tan��AOM=2Ϊ��ֵ����Ҫע�����۵��λ�ò�ͬʱ�����������Ȼ��������3������֪�����ǵ���ȹ�ϵ��BAE=��BED=��AOD�����Եõ���ABE�ס�OED����OE=a���������Ʊߵı�����ϵ���Եõ�m����x�ı���ʽm=��
=tan��AOM=2Ϊ��ֵ����Ҫע�����۵��λ�ò�ͬʱ�����������Ȼ��������3������֪�����ǵ���ȹ�ϵ��BAE=��BED=��AOD�����Եõ���ABE�ס�OED����OE=a���������Ʊߵı�����ϵ���Եõ�m����x�ı���ʽm=�� ![]() a2+
a2+ ![]() a��0��a��3
a��0��a��3 ![]() ��������һ�����κ����������˶��κ���ͼ�����ͼ3�����ɼ�m�ڲ�ͬȡֵ��Χʱ��a��ȡֵ����OE�ij��ȣ���E���λ�ã���1����2���������ͽ�����������ת��Ϊ�������κ�����ͼ�����������⣮���⣬�����������Ρ�ABE���OED�У������߶α�����ϵ֮ǰ��Ҫ�������AB�ij��ȣ����ͼ2������ͨ���������������Σ���������һ�κ�����ֱ�ߣ����������AB�ij��ȣ�
��������һ�����κ����������˶��κ���ͼ�����ͼ3�����ɼ�m�ڲ�ͬȡֵ��Χʱ��a��ȡֵ����OE�ij��ȣ���E���λ�ã���1����2���������ͽ�����������ת��Ϊ�������κ�����ͼ�����������⣮���⣬�����������Ρ�ABE���OED�У������߶α�����ϵ֮ǰ��Ҫ�������AB�ij��ȣ����ͼ2������ͨ���������������Σ���������һ�κ�����ֱ�ߣ����������AB�ij��ȣ�


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���P�������ߣ�y=x2�ϵĶ��㣨���ڵ�һ�����ڣ������� OP������0��OP�Ĵ��߽�����������һ��Q������PQ����y���ڵ�M����PA�Ax���ڵ�A��QB�Ax���ڵ�B�����P�ĺ�����Ϊm��
��1����ͼ1����m= ![]() ʱ��
ʱ��
�����߶�OP�ij���tan��POM��ֵ��
����y������һ��C��ʹ��OCQ����OQΪ���ĵ��������Σ����C�����ꣻ
��2����ͼ2������AM��BM���ֱ���OP��OQ�ཻ�ڵ�D��E��
���ú�m�Ĵ���ʽ��ʾ��Q�����ꣻ
����֤���ı���ODME�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У�AB��DC���߶�AG��BG�ֱ�CD�ڵ�E��F��DE=CF�� ��֤����GAB�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ��Ϊ�̳��˵�ʱ�У���������ͼ��ݵ����ã������˴������ߣ��йز���ͳ����2011��10����2012��3���ڼ䵽��ͼ��ݵĶ��ߵ�ְҵ�ֲ������ͳ��ͼ���£� 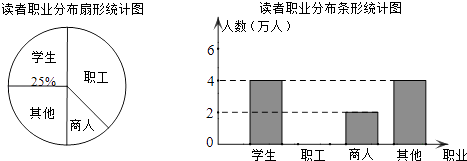
��1����ͳ�Ƶ����ʱ���ڣ��������˵���ͼ����Ķ�������������ռ�ٷֱ��� ��
��2��������ͳ��ͼ������������ܰ��ʾ����ͼʱ��������0.5�������ϵĺ�ɫǩ�ֱ�Ϳ�ڣ���
��3��������4�µ���ͼ��ݵĶ��߹�28000������������Լ�ж�����ְ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB�ڲ���˳�ε��������ߣ�OE��OC��OD��OF��OEƽ�֡�AOC��OFƽ�֡�DOB.
��1������AOB=160�㣬��COD=40�������EOF�Ķ�����
��2������AOB=a����COD=�������EOF�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
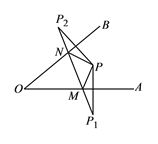
����Ŀ����ͼ��ʾ,��A0B=420����PΪ��A0B��һ�㣬�ֱ�����P�����OA��OB�ĶԳƵ�P1��P2������P1P2��OA��M����OB��N��P1P2=15������PMN���ܳ�Ϊ________����MPN ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ�ȱ������Σ�����B��BD��AC�ڵ�D����D��DE��BC����DE=CD������CE�� 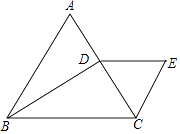
��1����֤����CDEΪ�ȱ������Σ�
��2��������BE����AB=4����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֱ��������ABC�Ƶ�A��ʱ����ת15���õ���AB��C�䣬��AC=1����ͼ����Ӱ���ֵ����Ϊ�� �� 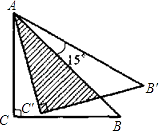
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=�� ![]() x2+
x2+ ![]() x+2��x�ύ�ڵ�A��B����y�ύ�ڵ�C����P���߶�BC�ϵĶ��㣨��P����B��C�غϣ������Ӳ��ӳ�AP������������һ��Q�����Q�ĺ�����Ϊx��
x+2��x�ύ�ڵ�A��B����y�ύ�ڵ�C����P���߶�BC�ϵĶ��㣨��P����B��C�غϣ������Ӳ��ӳ�AP������������һ��Q�����Q�ĺ�����Ϊx��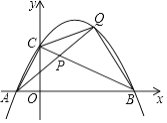
��1����д����A��B��C�����꣺A������B������C������
����֤����ABC��ֱ�������Σ�
��2���ǡ�BCQ�����ΪS����S����x�ĺ�������ʽ��
��3���ڵ�P���˶������У� ![]() �Ƿ�������ֵ�������ڣ����
�Ƿ�������ֵ�������ڣ���� ![]() �����ֵ����Q�����ꣻ�������ڣ���˵�����ɣ�
�����ֵ����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com