
【题目】在一次数学兴趣小组活动中,小明利用同弧所对的圆周角及圆心角的性质探索了一些问题,下面请你和小明一起进入探索之旅.
(1)如图1,△ABC中,∠A=30°,BC=2,则△ABC的外接圆的半径为 ;
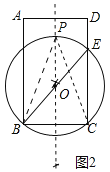
(2)如图2,在矩形ABCD中,请利用以上操作所获得的经验,在矩形ABCD内部用直尺与圆规作出一点P,点P满足;∠BPC=∠BEC,且PB=PC;(要求:用直尺与圆规作出点P,保留作图痕迹.)
(3)如图3,在平面直角坐标系的第一象限内有一点B,坐标为(2,m),过点B作AB⊥y轴,BC⊥x轴,垂足分别为A、C,若点P在线段AB上滑动(点P可以与点A、B重合),发现使得∠OPC=45°的位置有两个,则m的取值范围为 .
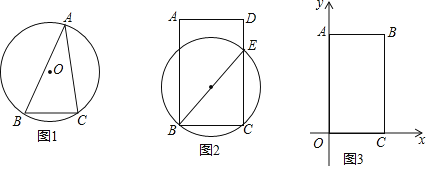
【答案】(1)2;(2)详见解析;(3)2≤m<1+![]() .
.
【解析】
(1)连接OB、OC,只要证明△OBC是等边三角形即可.
(2)如图2中,作BC的垂直平分线,交BE于点O,以O为圆心,OB为半径作圆,交垂直平分线于点P,则点P为所求.
(3)如图3中,在x轴上方作△OKC,使得△OKC是以OC为斜边的等腰直角三角形,作KE⊥AB于E.当EK=KC=![]() 时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+
时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+![]() ,在AB上只有一个点P满足∠OPC=
,在AB上只有一个点P满足∠OPC=![]() OKC=45°,当BK=
OKC=45°,当BK=![]() 时,在AB上恰好有两个点P满足∠OPC=
时,在AB上恰好有两个点P满足∠OPC=![]() OKC=45°,此时m=BC=2,由此不难得出结论.
OKC=45°,此时m=BC=2,由此不难得出结论.
(1)如图1中,连接OB、OC.
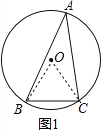
∵∠BOC=2∠A,∠A=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=2;
(2)如图2中,作BC的垂直平分线,交BE于点O;
以O为圆心,OB为半径作圆,交垂直平分线于点P,
则点P为所求.
(3)如图3中,在x轴上方作△OKC,使得△OKC是以OC为斜边的等腰直角三角形,作KE⊥AB于E.
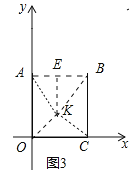
∵OC=2,
∴OK=KC=![]() ,
,
当EK=KC=![]() 时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+
时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+![]() ,在AB上只有一个点P满足∠OPC=
,在AB上只有一个点P满足∠OPC=![]() OKC=45°,
OKC=45°,
当BK=![]() 时,在AB上恰好有两个点P满足∠OPC=
时,在AB上恰好有两个点P满足∠OPC=![]() OKC=45°,此时m=BC=2,
OKC=45°,此时m=BC=2,
综上所述,满足条件的m的值的范围为2≤m<1+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O'A'BC'是矩形OABC绕B点逆时针旋转得到的.O'点恰好在x轴的正半轴上, O'C'交AB于点D.
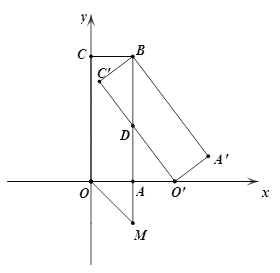
(1)求点O'的坐标,并判断△O'DB的形状(要说明理由)
(2)求边C'O'所在直线的解析式.
(3)延长BA到M使AM=1,在(2)中求得的直线上是否存在点P,使得ΔPOM是以线段OM为直角边的直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,AC=8cm,AB=12cm,点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,速度均为1cm/s.以AQ、PQ为边作AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤6).解答下列问题:
(1)当t为何值时,AQPD为矩形.
(2)当t为何值时,AQPD为菱形.
(3)是否存在某一时刻t,使四边形AQPD的面积等于四边形PQCB的面积,若存在,请求出t值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足![]() ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
,则点P到B、C两点距离之和最小时,∠PBC的度数为( )

A.30°B.45°C.60°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC内接于⊙O,BC是⊙O的直径,点D是BC延长线上的一点,AD=AB,且∠ACB=2∠D,CD=2(如图1)

(1)求证:AD是⊙O的切线;
(2)AD= ;
(3)若点E是⊙O上的一点,AE与BC交于点F,且点E等分半圆BC时(如图2),求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分![]() 分,学生得分均为整数,成绩达到
分,学生得分均为整数,成绩达到![]() 分及
分及![]() 分以上为合格,达到
分以上为合格,达到![]() 分或
分或![]() 分为优秀.这次竞赛中甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示
分为优秀.这次竞赛中甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示

组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 |
|
|
|
|
|
乙组 |
|
|
|
|
|
(1)求出成绩统计分析表中![]() ,
,![]() 的值;
的值;
(2)小英同学说:“这次竞赛我得了![]() 分,在我们小组中排名属中游略上!”观察上面表格判断,小英是甲、乙哪个组的学生;
分,在我们小组中排名属中游略上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组,但乙组同学不同意甲组同学的说法,认为他们的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一幅长为60 cm,宽为40 cm的矩形风景画的四周镶一条相同宽度的纸边,制成一幅矩形挂图.若要使整个挂图的面积是3 500 cm2,设纸边的宽为x cm,则根据题意可列方程为( )

A. (60+x)(40+x)=3 500 B. (60+2x)(40+2x)=3 500
C. (60-x)(40-x)=3 500 D. (60-2x)(40-2x)=3 500
查看答案和解析>>
科目:初中数学 来源: 题型:
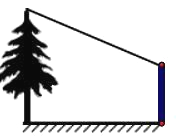
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一垛墙上,如图,此时测得地面上的影长为8米,墙上的影长为4米.同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com