
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЕФБпOAдкxжсе§АыжсЩЯЃЌБпOCдкyжсе§АыжсЩЯЃЌBЕуЕФзјБъЮЊ(1ЃЌ3)ЃЎОиаЮO'A'BC'ЪЧОиаЮOABCШЦBЕуФцЪБеыа§зЊЕУЕНЕФЃЎO'ЕуЧЁКУдкxжсЕФе§АыжсЩЯЃЌ O'C'НЛABгкЕуD.
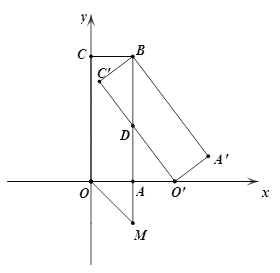
(1)ЧѓЕуO'ЕФзјБъЃЌВЂХаЖЯЁїO'DBЕФаЮзДЃЈвЊЫЕУїРэгЩЃЉ
(2)ЧѓБпC'O'ЫљдкжБЯпЕФНтЮіЪНЃЎ
(3)бгГЄBAЕНMЪЙAM=1ЃЌдк(2)жаЧѓЕУЕФжБЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУІЄPOMЪЧвдЯпЖЮOMЮЊжБНЧБпЕФжБНЧШ§НЧаЮ?ШєДцдкЃЌЧыжБНгаДГіPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)ЕуO'ЕФзјБъ(2ЃЌ0)ЃЌЁїO'DBЮЊЕШбќШ§НЧаЮЃЌРэгЩТдМћНтЮіЃЛ(2)БпC'O'ЫљдкжБЯпЕФНтЮіЪНЃК![]() ЃЛ (3)P(2,0)ЃЌ
ЃЛ (3)P(2,0)ЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгOBЃЌOЁфBЃЌИљОна§зЊЕФаджЪПЩЕУOB=OЁфBЃЌдйИљОнОиаЮЕФаджЪBAЁЭOAЃЌдйИљОнЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪПЩЕУAO=AOЁфЃЌШЛКѓИљОнЕуBЕФзјБъЧѓГіAOЕФГЄЖШЃЌдйЕУЕНAOЁфЕФГЄЖШЃЌЕуOЁфЕФзјБъМДПЩЕУЕНЃЛРћгУНЧНЧБпжЄУїЁїBCЁфDгыЁїOЁфADШЋЕШЃЌШЛКѓИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕУЕНBD=OЁфDЃЌЫљвдЁїOЁфDBЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉЩшЕуDЕФзјБъЪЧЃЈ1ЃЌaЃЉЃЌБэЪОГіOЁфDЕФГЄЖШЃЌШЛКѓРћгУЙДЙЩЖЈРэСаЪНЧѓГіaЕФжЕЃЌДгЖјЕУЕНЕуDЕФзјБъЃЌдйИљОнД§ЖЈЯЕЪ§ЗЈСаЪНМДПЩЧѓГіжБЯпCЁфOЁфЕФНтЮіЪНЃЛ
ЃЈ3ЃЉИљОнAM=1ПЩЕУЁїAOMЪЧЕШбќжБНЧШ§НЧаЮЃЌШЛКѓЗжЂйPMЪЧСэвЛжБНЧБпЃЌЁЯPMA=45ЁуЃЌЂкPOЪЧСэвЛжБНЧБпЃЌЁЯPOA=45ЁуСНжжЧщПіСаЪННјааМЦЫуМДПЩЕУНтЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌСЌНгOBЃЌOЁфBЃЌдђOB=OЁфBЃЌ
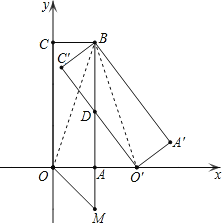
ЁпЫФБпаЮOABCЪЧОиаЮЃЌ
ЁрBAЁЭOAЃЌ
ЁрAO=AOЁфЃЌ
ЁпBЕуЕФзјБъЮЊЃЈ1ЃЌ3ЃЉЃЌ
ЁрOA=1ЃЌ
ЁрAOЁф=1ЃЌ
ЁрЕуOЁфЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЃЌ
ЁїOЁфDBЮЊЕШбќШ§НЧаЮЃЌ
РэгЩШчЯТЃКдкЁїBCЁфDгыЁїOЁфADжаЃЌ
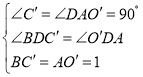
ЁрЁїBCЁфDЁеЁїOЁфADЃЈAASЃЉЃЌ
ЁрBD=OЁфDЃЌ
ЁрЁїOЁфDBЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉЩшЕуDЕФзјБъЮЊЃЈ1ЃЌaЃЉЃЌдђAD=aЃЌ
ЁпЕуBЕФзјБъЪЧЃЈ1ЃЌ3ЃЉЃЌ
ЁрOЁфD=3-aЃЌ
дкRtЁїADOЁфжаЃЌAD2+AOЁф2=OЁфD2ЃЌ
Ёрa2+12=ЃЈ3-aЃЉ2ЃЌ
НтЕУ![]()
ЁрЕуDЕФзјБъЮЊ![]()
ЩшжБЯпCЁфOЁфЕФНтЮіЪНЮЊy=kx+bЃЌ
дђ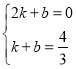 НтЕУ
НтЕУ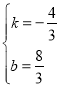
ЁрБпCЁфOЁфЫљдкжБЯпЕФНтЮіЪНЃК![]()
ЃЈ3ЃЉЁпAM=1ЃЌAO=1ЃЌЧвAMЁЭAOЃЌ
ЁрЁїAOMЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЂйPMЪЧСэвЛжБНЧБпЪБЃЌЁЯPMA=45ЁуЃЌ
ЁрPA=AM=1ЃЌЕуPгыЕуOЁфжиКЯЃЌ
ЁрЕуPЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЃЌ
ЂкPOЪЧСэвЛжБНЧБпЃЌЁЯPOA=45ЁуЃЌдђPOЫљдкЕФжБЯпЮЊy=xЃЌ
Ёр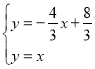
НтЕУ![]()
ЁрЕуPЕФзјБъЮЊPЃЈ2ЃЌ0ЃЉЛђ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() жаЃЌШчЙћЙ§ЯюЕу
жаЃЌШчЙћЙ§ЯюЕу![]() ЕФвЛЬѕжБЯпАбетИіШ§НЧаЮЗжИюГЩСНИіШ§НЧаЮЃЌЦфжавЛИіЮЊЕШбќШ§НЧаЮЃЌСэвЛИіЮЊжБНЧШ§НЧаЮЃЌдђГЦетЬѕжБЯпЮЊ
ЕФвЛЬѕжБЯпАбетИіШ§НЧаЮЗжИюГЩСНИіШ§НЧаЮЃЌЦфжавЛИіЮЊЕШбќШ§НЧаЮЃЌСэвЛИіЮЊжБНЧШ§НЧаЮЃЌдђГЦетЬѕжБЯпЮЊ![]() ЕФЙигкЕу
ЕФЙигкЕу![]() ЕФЖўЗжИюЯпЃЎР§ШчЃКШчЭМ1ЃЌ
ЕФЖўЗжИюЯпЃЎР§ШчЃКШчЭМ1ЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШєЙ§ЖЅЕу
ЃЌШєЙ§ЖЅЕу![]() ЕФвЛЬѕжБЯп
ЕФвЛЬѕжБЯп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЯдШЛжБЯп
ЃЌЯдШЛжБЯп![]() ЪЧ
ЪЧ![]() ЕФЙигкЕу
ЕФЙигкЕу![]() ЕФЖўЗжИюЯпЃЎ
ЕФЖўЗжИюЯпЃЎ
ЃЈ1ЃЉдкЭМ2ЕФ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЧыдкЭМ2жаЛГі
ЃЎЧыдкЭМ2жаЛГі![]() ЙигкЕу
ЙигкЕу![]() ЕФЖўЗжИюЯпЃЌЧв
ЕФЖўЗжИюЯпЃЌЧв![]() НЧЖШЪЧ ЃЛ
НЧЖШЪЧ ЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌдкЭМ3жаЛГіВЛЭЌгкЭМ1ЃЌЭМ2ЕФ
ЃЌдкЭМ3жаЛГіВЛЭЌгкЭМ1ЃЌЭМ2ЕФ![]() ЃЌЫљЛ
ЃЌЫљЛ![]() ЭЌЪБТњзу:Ђй
ЭЌЪБТњзу:Ђй![]() ЮЊзюаЁНЧЃЛЂкДцдкЙигкЕу
ЮЊзюаЁНЧЃЛЂкДцдкЙигкЕу![]() ЕФЖўЗжИюЯпЃЎ
ЕФЖўЗжИюЯпЃЎ![]() ЕФЖШЪ§ЪЧ ЃЛ
ЕФЖШЪ§ЪЧ ЃЛ
ЃЈ3ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЭЌЪБТњзуЃКЂй
ЭЌЪБТњзуЃКЂй![]() ЮЊзюаЁНЧЃЛЂкДцдкЙигкЕу
ЮЊзюаЁНЧЃЛЂкДцдкЙигкЕу![]() ЕФЖўЗжИюЯпЃЎЧыЧѓГі
ЕФЖўЗжИюЯпЃЎЧыЧѓГі![]() ЕФЖШЪ§ЃЈгУ
ЕФЖШЪ§ЃЈгУ![]() БэЪОЃЉЃЎ
БэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
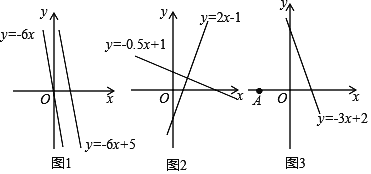
ЁОЬтФПЁПВФСЯвЛЃКШчЭМ1ЃЌгЩПЮБО91вГР§2ЛКЏЪ§yЃНЉ6xгыyЃНЉ6x+5ПЩжЊЃЌжБЯпyЃНЉ6x+5ПЩвдгЩжБЯпyЃНЉ6xЯђЩЯЦНвЦ5ИіЕЅЮЛГЄЖШЕУЕНгЩДЫЮвУЧЕУЕНе§ШЗЕФНсТлвЛЃКдкжБЯпL1ЃКy=K1x+b1гыжБЯпL2ЃКy=K2x+b2жаЃЌШчЙћK1=K2 Чвb1Ёйb2 ЃЌФЧУДL1ЁЮL2ЃЌЗДЙ§РДЃЌвВГЩСЂЃЎ
ВФСЯЖўЃКШчЭМ2ЃЌгЩПЮБО92вГР§3ЛКЏЪ§yЃН2xЉ1гыyЃНЉ0.5x+1ПЩжЊЃЌРћгУЫљбЇжЊЪЖвЛЖЈФмжЄГіетСНЬѕжБЯпЪЧЛЅЯрДЙжБЕФЃЎгЩДЫЮвУЧЕУЕНе§ШЗЕФНсТлЖўЃКдкжБЯпL1ЃКy=k1x+b1 гыL2ЃКy=k2x+b2 жаЃЌШчЙћk1ЁЄk2=-1ФЧУДL1ЁЭL2ЃЌЗДЙ§РДЃЌвВГЩСЂ
гІгУОйР§
вбжЊжБЯпyЃНЉ![]() x+5гыжБЯпyЃНkx+2ЛЅЯрДЙжБЃЌдђЉ
x+5гыжБЯпyЃНkx+2ЛЅЯрДЙжБЃЌдђЉ![]() kЃНЉ1ЃЎЫљвдkЃН6
kЃНЉ1ЃЎЫљвдkЃН6
НтОіЮЪЬт
(1)ЧыаДГівЛЬѕжБЯпНтЮіЪН______ЃЌЪЙЫќгыжБЯпyЃНxЉ3ЦНааЃЎ
(2)ШчЭМ3ЃЌЕуAзјБъЮЊ(Љ1ЃЌ0)ЃЌЕуPЪЧжБЯпyЃНЉ3x+2ЩЯвЛЖЏЕуЃЌЕБЕуPдЫЖЏЕНКЮЮЛжУЪБЃЌЯпЖЮPAЕФГЄЖШзюаЁЃПВЂЧѓГіДЫЪБЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
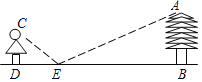
ЁОЬтФПЁПЮЊСЫВтСПаЃдАФквЛПУВЛПЩХЪЕФЪїЕФИпЖШЃЌбЇаЃЪ§бЇгІгУЪЕМљаЁзщзіСЫШчЯТЕФЬНЫїЃКИљОнЙтЕФЗДЩфЖЈТЩЃЌРћгУвЛУцОЕзгКЭЦЄГпЃЌЩшМЦШчЭМЫљЪОЕФВтСПЗНАИЃКАбОЕзгЗХдкРыЪїABЕФЪїИљ7.2mЕФЕуEДІЃЌШЛКѓЙлВтепбизХжБЯпBEКѓЭЫЕНЕуDЃЌетЪБЧЁКУдкОЕзгРяПДЕНЪїЩвЖЅЕуAЃЌдйгУЦЄГпСПЕУDE=2.4mЃЌЙлВтепФПИпCD=1.6mЃЌдђЪїИпABдМЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙЄШЫЪІИЕгУвЛПщГЄЮЊ2mЃЌПэЮЊ1.2mЕФОиаЮЬњЦЄжЦзївЛИіЮоИЧЕФГЄЗНЬхШнЦїЃЌашвЊНЋЫФНЧИїВУЕєвЛИіе§ЗНаЮЃЎЃЈКёЖШВЛМЦЃЉ
ЃЈ1ЃЉШєГЄЗНЬхЕзУцУцЛ§ЮЊ1.28m2ЃЌЧѓВУЕєЕФе§ЗНаЮБпГЄЃЛ
ЃЈ2ЃЉШєвЊЧѓжЦзїЕФГЄЗНЬхЕФЕзУцГЄВЛДѓгкЕзУцПэЕФ3БЖЃЌВЂНЋШнЦїНјааЗРатДІРэЃЌВрУцУПЦНЗНУзЕФЗбгУЮЊ50дЊЃЌЕзУцУПЦНЗНУзЕФЗбгУЮЊ200дЊЃЌВУЕєЕФе§ЗНаЮБпГЄЖрДѓЪБЃЌзмЗбгУзюЕЭЃЌзюЕЭЮЊЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКжБЯп![]() ЃЌ
ЃЌ![]() ЮЊЭМаЮФквЛЕуЃЌСЌНг
ЮЊЭМаЮФквЛЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌаДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
жЎМфЕФЕШСПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЧыжБНгаДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЙиЯЕЪНЃЛ
жЎМфЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉФуЛЙФмОЭБОЬтзїГіЪВУДаТЕФВТЯыЃПЧыЛЭМВЂаДГіФуЕФНсТлЃЈВЛБижЄУїЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
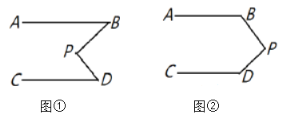
ЁОЬтФПЁПгаЙЋТЗl1ЭЌВрЁЂl2вьВрЕФСНИіГЧеђAЃЌBЃЌШчЯТЭМЃЎЕчаХВПУХвЊаоНЈвЛзљаХКХЗЂЩфЫўЃЌАДееЩшМЦвЊЧѓЃЌЗЂЩфЫўЕНСНИіГЧеђAЃЌBЕФОрРыБиаыЯрЕШЃЌЕНСНЬѕЙЋТЗl1ЃЌl2ЕФОрРывВБиаыЯрЕШЃЌЗЂЩфЫўCгІаоНЈдкЪВУДЮЛжУЃПЧыгУГпЙцзїЭМевГіЫљгаЗћКЯЬѕМўЕФЕуЃЌзЂУїЕуCЕФЮЛжУЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛвЊЧѓаДГіЛЗЈЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛДЮЪ§бЇаЫШЄаЁзщЛюЖЏжаЃЌаЁУїРћгУЭЌЛЁЫљЖдЕФдВжмНЧМАдВаФНЧЕФаджЪЬНЫїСЫвЛаЉЮЪЬтЃЌЯТУцЧыФуКЭаЁУївЛЦ№НјШыЬНЫїжЎТУЃЎ
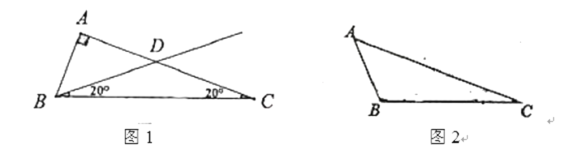
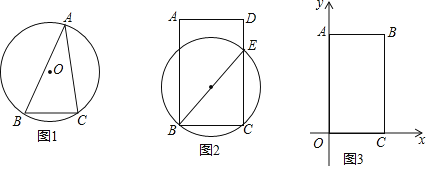
ЃЈ1ЃЉШчЭМ1ЃЌЁїABCжаЃЌЁЯA=30ЁуЃЌBC=2ЃЌдђЁїABCЕФЭтНгдВЕФАыОЖЮЊ ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкОиаЮABCDжаЃЌЧыРћгУвдЩЯВйзїЫљЛёЕУЕФОбщЃЌдкОиаЮABCDФкВПгУжБГпгыдВЙцзїГівЛЕуPЃЌЕуPТњзуЃЛЁЯBPC=ЁЯBECЃЌЧвPB=PCЃЛЃЈвЊЧѓЃКгУжБГпгыдВЙцзїГіЕуPЃЌБЃСєзїЭМКлМЃЃЎЃЉ
ЃЈ3ЃЉШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕЕФЕквЛЯѓЯоФкгавЛЕуBЃЌзјБъЮЊЃЈ2ЃЌmЃЉЃЌЙ§ЕуBзїABЁЭyжсЃЌBCЁЭxжсЃЌДЙзуЗжБ№ЮЊAЁЂCЃЌШєЕуPдкЯпЖЮABЩЯЛЌЖЏЃЈЕуPПЩвдгыЕуAЁЂBжиКЯЃЉЃЌЗЂЯжЪЙЕУЁЯOPC=45ЁуЕФЮЛжУгаСНИіЃЌдђmЕФШЁжЕЗЖЮЇЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕчЖЏздааГЕвбГЩЮЊЪаУёШеГЃГіааЕФЪзбЁЙЄОпЁЃОнФГЪаЦЗХЦЕчЖЏздааГЕОЯњЩЬ1жС3дТЗнЭГМЦЃЌИУЦЗХЦЕчЖЏздааГЕ1дТЗнЯњЪл150СОЃЌ3дТЯњЪл216СО.
ЃЈ1ЃЉЧѓИУЦЗХЦЕчЖЏГЕЯњЪлСПЕФдТЦНОљдіГЄТЪЃЛ
ЃЈ2ЃЉШєИУЦЗХЦЕчЖЏздааГЕЕФНјМлЮЊ2300дЊЃЌЪлМл2800дЊЃЌдђИУОЯњЩЬ1дТжС3дТЙВгЏРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com