
【题目】如图,△ABC中,AD垂直BC于点D,且AD=BC,BC上方有一动点P满足![]() ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
,则点P到B、C两点距离之和最小时,∠PBC的度数为( )

A.30°B.45°C.60°D.90°
【答案】B
【解析】
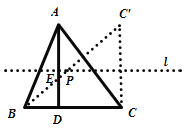
根据![]() 得出点P到BC的距离等于AD的一半,即点P在过AD的中点且平行于BC的直线l上,则此问题转化成在直线l上求作一点P,使得点P到B、C两点距离之和最小,作出点C关于直线l的对称点C’,连接BC’,然后根据条件证明△BCC’是等腰直角三角形即可得出∠PBC的度数.
得出点P到BC的距离等于AD的一半,即点P在过AD的中点且平行于BC的直线l上,则此问题转化成在直线l上求作一点P,使得点P到B、C两点距离之和最小,作出点C关于直线l的对称点C’,连接BC’,然后根据条件证明△BCC’是等腰直角三角形即可得出∠PBC的度数.
解:∵![]() ,
,
∴点P到BC的距离=![]() AD,
AD,
∴点P在过AD的中点E且平行于BC的直线l上,
作C点关于直线l的对称点C’,连接BC’,交直线l于点P,
则点P即为到B、C两点距离之和最小的点,
∵AD⊥BC,E为AD的中点,l∥BC,点C和点C’关于直线l对称,
∴CC’=AD=BC,CC’⊥BC,
∴三角形BCC’是等腰直角三角形,
∴∠PBC=45°.
故选B.


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
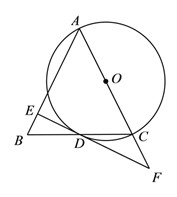
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
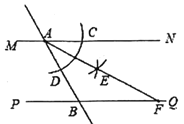
【题目】如图,直线![]() ,直线
,直线![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() 、
、![]() ,小宇同学利用尺规按以下步骤作图:①以点
,小宇同学利用尺规按以下步骤作图:①以点![]() 为圆心,以任意长为半径作弧交
为圆心,以任意长为半径作弧交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ②分别以
②分别以![]() ,
,![]() 为圆心,以大于,
为圆心,以大于,![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ____________.
____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
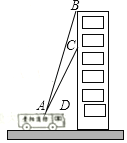
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某校要求没有读过四大名著的学生进行选读,将《西游记》、《三国演义》、《水浒传》《红楼梦》依次记为A、B、C、D,每本名著被选到的机会均等.
(1)学生小红计划选读两本名著,她恰好选读《西游记》和《水浒传》这两本名著的概率为多少?
(2)若学生小明和小刚各计划选读一本名著,他们两人恰好选读同一本名著的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
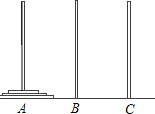
【题目】如图A、B、C是固定在桌面上的三根立柱,其中A柱上穿有三个大小不同的圆片,下面的直径总比上面的大![]() 现想将这三个圆片移动到B柱上,要求每次只能移动一片
现想将这三个圆片移动到B柱上,要求每次只能移动一片![]() 叫移动一次
叫移动一次![]() ,被移动的圆片只能放入A、B、C三个柱之一且较大的圆片不能叠在小片的上面,那么完成这件事情至少要移动圆片的次数是
,被移动的圆片只能放入A、B、C三个柱之一且较大的圆片不能叠在小片的上面,那么完成这件事情至少要移动圆片的次数是![]()
![]()
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com