
【题目】如图,已知Rt△ABC中,∠C=90°,AC=8cm,AB=12cm,点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,速度均为1cm/s.以AQ、PQ为边作AQPD,连接DQ,交AB于点E.设运动的时间为t(单位:s)(0≤t≤6).解答下列问题:
(1)当t为何值时,AQPD为矩形.
(2)当t为何值时,AQPD为菱形.
(3)是否存在某一时刻t,使四边形AQPD的面积等于四边形PQCB的面积,若存在,请求出t值,若不存在,请说明理由.

【答案】(1) 当t=![]() 时,AQPD是矩形;(2) 当t=
时,AQPD是矩形;(2) 当t=![]() 时,□AQPD是菱形;(3)
时,□AQPD是菱形;(3) ![]()
【解析】
(1)利用矩形的性质得到△APQ∽△ABC,利用相似三角形对应边的比相等列出比例式即可求得t值;
(2)利用菱形的对角线相互垂直平分解答;
(3)过点P作PM⊥AC于M.先表示出△APQ的面积和S四边形PQCB=S△ABC﹣S△APQ,进而建立方程即可得出结论.
解:(1)如图2,当AQPD是矩形时,PQ⊥AC,
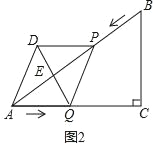
∴PQ∥BC,
∴△APQ∽△ABC
∴![]() =
=![]() ,
,
由运动知,QA=t,BP=t,
∴AP=AB﹣BP=12﹣t,
即,![]() =
=![]() ,
,
解之 t=![]() ,
,
∴当t=![]() 时,AQPD是矩形;
时,AQPD是矩形;
(2)当AQPD是菱形时,DQ⊥AP,AE=![]() AP
AP
则 cos∠BAC=![]() =
=![]() ,
,
由运动知,QA=t,BP=t,
∴AP=AB﹣BP=12﹣t,AE=6﹣![]() t,
t,
∴![]()
解之 t=![]() ,
,
所以当t=![]() 时,□AQPD是菱形;
时,□AQPD是菱形;
(3)存在时间t,使四边形AQPD的面积等于四边形PQCB的面积.
在Rt△ABC中,根据勾股定理得,BC=4![]() ,
,
如图3,过点P作PM⊥AC于M.
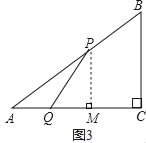
则![]() =
=![]() ,
,
即![]() =
=![]() ,
,
故PM=![]() (12﹣t).
(12﹣t).
∴S△APQ=![]() AQ×PM=
AQ×PM=![]() ×t×
×t×![]() (12﹣t),
(12﹣t),
∴S四边形PQCB=S△ABC﹣S△APQ=![]() ×4
×4![]() ×8﹣
×8﹣![]() ×t×
×t×![]() (12﹣t),
(12﹣t),
∵四边形AQPD的面积等于四边形PQCB的面积,
∴2×![]() ×t×
×t×![]() (12﹣t)=
(12﹣t)=![]() ×4
×4![]() ×8﹣
×8﹣![]() ×t×
×t×![]() (12﹣t),
(12﹣t),
∴t=![]() (舍)或t=
(舍)或t=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣5交y轴于点A,交x轴于点B(﹣5,0)和点C(1,0),过点A作AD∥x轴交抛物线于点D.
(1)求此抛物线的表达式;
(2)点E是抛物线上一点,且点E关于x轴的对称点在直线AD上,求△EAD的面积;
(3)若点P是直线AB下方的抛物线上一动点,当点P运动到某一位置时,△ABP的面积最大,求出此时点P的坐标和△ABP的最大面积.
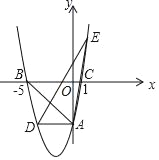
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离树AB的树根7.2m的点E处,然后观测者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4m,观测者目高CD=1.6m,则树高AB约是__________.
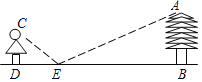
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,
,![]() 为图形内一点,连接
为图形内一点,连接![]() ,
,![]() .
.
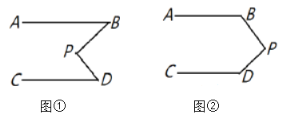
(1)如图①,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论;
之间的等量关系,并证明你的结论;
(2)如图②,请直接写出![]() ,
,![]() ,
,![]() 之间的关系式;
之间的关系式;
(3)你还能就本题作出什么新的猜想?请画图并写出你的结论(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线![]() 、
、![]() 交于点
交于点![]() ,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①
,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①![]() ⊥
⊥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,可以使这个新的四边形成为矩形,那么这样的条件个数是()
,可以使这个新的四边形成为矩形,那么这样的条件个数是()

A. 1个;B. 2个;
C. 3个;D. 4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,小明利用同弧所对的圆周角及圆心角的性质探索了一些问题,下面请你和小明一起进入探索之旅.
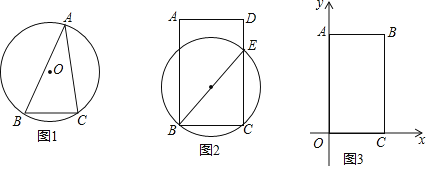
(1)如图1,△ABC中,∠A=30°,BC=2,则△ABC的外接圆的半径为 ;
(2)如图2,在矩形ABCD中,请利用以上操作所获得的经验,在矩形ABCD内部用直尺与圆规作出一点P,点P满足;∠BPC=∠BEC,且PB=PC;(要求:用直尺与圆规作出点P,保留作图痕迹.)
(3)如图3,在平面直角坐标系的第一象限内有一点B,坐标为(2,m),过点B作AB⊥y轴,BC⊥x轴,垂足分别为A、C,若点P在线段AB上滑动(点P可以与点A、B重合),发现使得∠OPC=45°的位置有两个,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
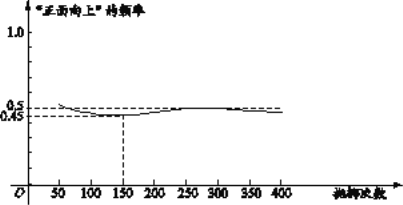
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com