
����Ŀ����ͼ��ֱ��y=��![]() x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��������y=��
x+c��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B��������y=��![]() x2+bx+c������A��B��
x2+bx+c������A��B��
��1�����B������������ߵĽ���ʽ��
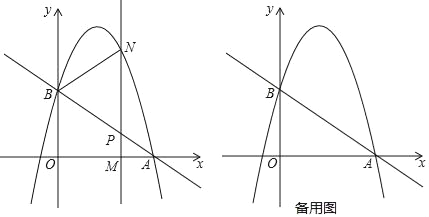
��2��M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N��
�ٵ�M���߶�OA���˶�������B��P��NΪ���������������APM���ƣ����M�����ꣻ
�ڵ�M��x���������˶�����������M��P��N��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����M��P��N����Ϊ����г��������ֱ��д��ʹ��M��P��N�����Ϊ����г������m��ֵ��
���𰸡�(1)�����߽���ʽΪy=��![]() x2+
x2+![]() x+2��(2)�ٵ�M������Ϊ��2.5��0����
x+2��(2)�ٵ�M������Ϊ��2.5��0����![]() ��0������m��ֵΪ
��0������m��ֵΪ![]() ��1��
��1��![]() ��
��
�������������������1����A���������ֱ�߽���ʽ�����c��������B�����꣬��A��B�����꣬���ô���ϵ��������������߽���ʽ��
��2������M������ɱ�ʾP��N�����꣬�Ӷ��ɱ�ʾ��MA��MP��PN��PB�ij�������NBP=90������BNP=90������������ֱ��������������ε����ʿɵõ�����m�ķ��̣������m��ֵ��
����m�ɱ�ʾ��M��P��N�����꣬�������֪��PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬�ɷֱ�õ�����m�ķ��̣������m��ֵ��
����������⣺
��1����![]() ��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B����0=��2+c�����c=2����B��0��2������������
��x�ύ�ڵ�A��3��0������y�ύ�ڵ�B����0=��2+c�����c=2����B��0��2������������![]() ������A��B����
������A��B����![]() �������
������� 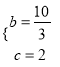 ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2�����ɣ�1����ֱ֪�߽���ʽΪ![]() ����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N����P��m��
����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N����P��m�� ![]() ����N��m��
����N��m�� ![]() ������PM=
������PM=![]() ��PA=3��m��PN=
��PA=3��m��PN=![]() ����
����![]() ��=
��=![]() ���ߡ�BPN����APM���ƣ�����BPN=��APM�����BNP=��AMP=90������NBP=��AMP=90���������������
���ߡ�BPN����APM���ƣ�����BPN=��APM�����BNP=��AMP=90������NBP=��AMP=90���������������
����BNP=90��ʱ������BN��MN�����N��������Ϊ2���� ![]() =2�����m=0����ȥ����m=
=2�����m=0����ȥ����m=![]() ����M��
����M��![]() ��0����
��0����
����NBP=90��ʱ������![]() ����A��3��0����B��0��2����P��m��
����A��3��0����B��0��2����P��m�� ![]() ������BP=
������BP=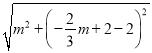 =
= ![]() ��AP=
��AP=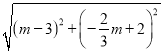 =
=![]() ��3��m������
��3��m������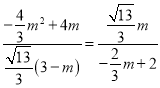 �����m=0����ȥ����m=
�����m=0����ȥ����m=![]() ����M��
����M��![]() ��0����
��0����
���Ͽ�֪����B��P��NΪ���������������APM����ʱ����M������Ϊ��![]() ��0����
��0����![]() ��0����
��0����
��������֪M��m��0����P��m�� ![]() ����N��m��
����N��m�� ![]() ������M��P��N����Ϊ����г����������PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬��PΪ�߶�MN���е�ʱ������2��
������M��P��N����Ϊ����г����������PΪ�߶�MN���е㡢MΪ�߶�PN���е��NΪ�߶�PM���е㣬��PΪ�߶�MN���е�ʱ������2��![]() ��=
��=![]() �����m=3�������غϣ���ȥ����m=
�����m=3�������غϣ���ȥ����m=![]() ��
��
��MΪ�߶�PN���е�ʱ������![]() +��
+��![]() ��=0�����m=3����ȥ����m=��1��
��=0�����m=3����ȥ����m=��1��
��NΪ�߶�PM���е�ʱ������![]() =2��
=2��![]() �������m=3����ȥ����m=
�������m=3����ȥ����m=![]() ��
��
���Ͽ�֪��M��P��N�����Ϊ����г����ʱm��ֵΪ![]() ��1��
��1��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������е�3������6��2��8���Ƚ��������ڵ��������������ұ�ȥ��ߵ���������֮��д����������֮�䣬�ɲ���һ���µ�������6��-4��2��6��8���Ϊ��һ�β��������ڶ���ͬ��������Ҳ�ɲ���һ����������6��-10��-4��6��2��4��6��2��8���������β�����ȥ���ʣ���������6��2��8��ʼ������2019�κ����������Ǹ���������������֮����( )
A.4054B.4056C.4058D.4060
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���������ij�ֹ�Ʊ1000�ɣ�ÿ��27Ԫ��

��1������������ʱ��ÿ���Ƕ���Ԫ��
��2�������������ÿ�ɶ���Ԫ����ͼ���ÿ�ɶ���Ԫ��
��3����С���ڱ���������̼۽���Ʊȫ������������Ϊ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��![]() ������ͬһֱ���ϣ�
������ͬһֱ���ϣ�![]() .
.
��1����֪��![]() ��ֱ��
��ֱ��![]() �ϣ������������벹������ͼ�Σ�����
�ϣ������������벹������ͼ�Σ�����![]() �ij���
�ij���
![]()
��2����֪��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬�����������벹������ͼ�Σ�����
���е㣬�����������벹������ͼ�Σ�����![]() �ij���ֱ��д��
�ij���ֱ��д��![]() ��
��![]() �ij����ڵ�������ϵ��
�ij����ڵ�������ϵ��
![]()
��3����֪��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬�����������벹������ͼ�Σ�����
���е㣬�����������벹������ͼ�Σ�����![]() �ij���ֱ��д��
�ij���ֱ��д��![]() ��
��![]() �ij����ڵ�������ϵ.
�ij����ڵ�������ϵ.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=![]() Ϊ������������
������������
��1����k��ֵ��
��2������ͼ���ڵ��� �������ڣ��ڸ������ڣ�y��x������� ��������仯�����
��3�������2��x����![]() ʱ��y��ȡֵ��Χ��
ʱ��y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��
��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��
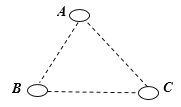
A.�ڡ�A����B���ڽ�ƽ���ߵĽ��㴦
B.��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
C.��AC��BC���߸��ߵĽ��㴦
D.��AC��BC�������ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD������BEC��ƽ�����Ƶ�B��ת60�����ã���AB��BC��BE��CE������DE.
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и��⣺
(1)(��12.5)��20.5��
(2)2![]() ��(��
��(��![]() )��
)��
(3)10��2��![]() ��(��2)��
��(��2)��
(4)1��(1��0.5)��![]() ��[2��(��2)2]��
��[2��(��2)2]��
(5)��52��(��2)��![]() 2��
2��
(6)��22��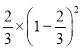 ��
��
(7)17��23��(��2)��3��
(8)2��(��5)��23��3��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��˫����![]() �ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ������˫���ߵ���һ��֧���ڵ�B����ABΪ�ױ�������ֱ��������ABC��ʹ�õ�Cλ�ڵ������ޡ�
�ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ������˫���ߵ���һ��֧���ڵ�B����ABΪ�ױ�������ֱ��������ABC��ʹ�õ�Cλ�ڵ������ޡ�
��1����C��ԭ��O����̾�����________��
��2��û��C������Ϊ��![]()
![]() ����A���˶��Ĺ����У�y��x�ı仯���仯��y����x�ĺ�����ϵʽΪ________��
����A���˶��Ĺ����У�y��x�ı仯���仯��y����x�ĺ�����ϵʽΪ________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com