
����Ŀ����ͼ1��ֱ��DE����һ��O������O��ֱ��DE�Ϸ�������OC����COE��140�㣬��һֱ�����ǰ�AOB��ֱ�Ƕ�����ڵ�O����һ��ֱ�DZ�OA������OD�ϣ���һ��OB��ֱ��DE�Ϸ�����ֱ�����ǰ����ŵ�O��ÿ��10����ٶ���ʱ����תһ�ܣ�����תʱ��Ϊt�룮
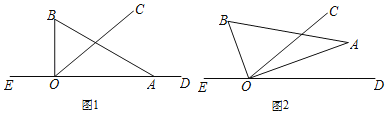
��1����ֱ�����ǰ���ת����ͼ2��λ��ʱ��OAǡ��ƽ�֡�COD�����ʱ��BOC�Ķ�����
��2��������OC��λ�ñ��ֲ��䣬����ת�����У��Ƿ����ij��ʱ�̣�ʹ������OA��OC��OD�е�ijһ���������������������ɼнǵĽ�ƽ���ߣ������ڣ������t��ȡֵ���������ڣ���˵�����ɣ�
��3���������ǰ忪ʼת����ͬʱ������OCҲ��O����ÿ��15����ٶ���ʱ����תһ�ܣ�����ת��ʼ�ʱ�䣬����OCƽ�֡�BOD��ֱ��д��t��ֵ���������еĽǾ�Ϊ����0����С��180��Ľǣ�
���𰸡���1����BOC��70�㣻��2�����ڣ�t��2��t��8��32����3��![]() ��
��![]() .
.
��������
��1����ͼ��֪��BOC����AOB����AOC����AOC�����ý�ƽ����ƽ�ǵĶ������.
��2����OAƽ����COD��OCƽ����AOD��ODƽ����AOC��������ֱ�������ۣ���������t�ķ��̣��ⷽ�̼���.
��3���ֱ��ú�t�Ĵ���ʽ��ʾ����COD�͡�BOD���ٸ���OCƽ�֡�BOD�������̽ⷽ�̼��ɣ�ע����������.
��1���⣺�ߡ�COE��140�㣬
���COD��180�㩁��COE��40�㣬
����OAƽ����COD��
���AOC��![]() ��COD��20�㣬
��COD��20�㣬
�ߡ�AOB��90�㣬
���BOC��90�㩁��AOC��70�㣻
��2������
����OAƽ����CODʱ����AOD����AOC����10��t��20�㣬��ã�t��2��
����OCƽ����AODʱ����AOC����DOC����10��t��40�㣽40�㣬��ã�t��8��
����ODƽ����AOCʱ����AOD����COD����360�㩁10��t��40�㣬��ã�t��32��
����������t��2��t��8��32��
��3��![]() ��
��![]() ���������£�
���������£�
���˶�ʱ��Ϊt������
����90+10t��2��40+15t��ʱ��t��![]()

����270��10t��2��320��15t��ʱ��t��![]()

����t��ֵΪ![]() ��
��![]() ��
��


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOC���BOC���࣬ODƽ�֡�BOC����AOE��2��COE������DOE��36�������EOC�Ķ�����
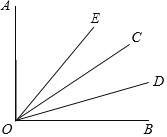
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
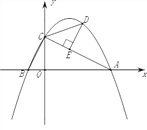
����Ŀ����ֱ֪��y����![]() x��2��x�ᡢy��ֱ��ڵ�A��C��������y=��
x��2��x�ᡢy��ֱ��ڵ�A��C��������y=��![]() x2��bx��c����A��C������x�ύ����һ��B���ڵ�һ��������������ȡһ��D���ֱ�����CD��AD����
x2��bx��c����A��C������x�ύ����һ��B���ڵ�һ��������������ȡһ��D���ֱ�����CD��AD����![]() �ڵ�E��
�ڵ�E��
(1)�������ߵı���ʽ��
(2)����ACD��������ֵ��
(3)����CED����COB���ƣ����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ֱ�������֩�3��1��3�IJ�����Ƭ�����dz������ⶼ��ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ������س�ȡһ�ţ��Żؿ�Ƭϴ�Ⱥ��ٴ����ſ�Ƭ������س�ȡһ�ţ�
��1�������б�����״ͼ�ķ����������γ�ȡ�Ŀ�Ƭ�ϵ�����֮��Ϊ�����ĸ��ʣ�
��2�������γ�ȡ�Ŀ�Ƭ�ϵ�����֮��Ϊ�Ǹ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB��20����C��BA���ӳ����ϣ���D��ֱ��AB�ϣ�AC��12��BD��16����M���߶�CD���е㣬��AM�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ���������С���ھ��꼶�����ȡ��һ����ѧ������ĩ��ѧ�ɼ�Ϊ��������ΪA��100��90�֣���B��89��80�֣���C��79��60�֣���D��59��0�֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ����������⣺
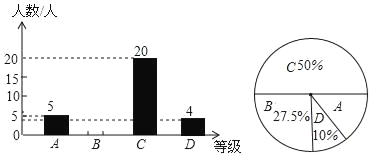
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ��1200�ˣ�������Ϊ80�֣���80�֣�����Ϊ���㣬�������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ�ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
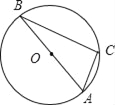
����Ŀ����ͼ����O����ABC���Բ��ֱ��AB=12����A=2��B��
��1����A=�� ���㣬��B=�� ���㣻
��2����BC�ij�������ø��ű�ʾ����
��3������OC���ӳ�����P��ʹCP=OC������PA������ͼ�Σ���֤��PA�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ����
����![]() ��AB���ϵĵ�D˳ʱ����ת
��AB���ϵĵ�D˳ʱ����ת![]() �õ�
�õ�![]() ��AB�ڵ�E����
��AB�ڵ�E����![]() ����
����![]() �������
�������![]()
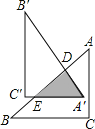
A. 3 B. 5 C. 11 D. 6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com