
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能完全地写出来,于是小明用
的小数部分我们不可能完全地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,用这个数减去其整数部分,差就是小数部分.
的整数部分是1,用这个数减去其整数部分,差就是小数部分.
请解答下列问题:
(1)求出![]() +2的整数部分和小数部分;
+2的整数部分和小数部分;
(2)已知:10+![]() =x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再回答问题:如果x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2 , x1x2与系数a、b、c的关系是:x1+x2= ![]() ,
, ![]() ,例如:若x1、x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣
,例如:若x1、x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣ ![]() =
= ![]()
![]() ,x1x2=
,x1x2= ![]() .若x1、x2是方程2x2+x﹣3=0的两个根.
.若x1、x2是方程2x2+x﹣3=0的两个根.
(1)求x1+x2 , x1x2;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数 ![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数 ![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.
(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数 ![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用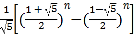 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.

任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.
(1)说明△ADE≌△CFE;
(2)判断线段AB、CF、BD之间的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com