
分析 (1)类比给出的方法得出$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)利用给出的方法拆分计算即可;
(3)提取$\frac{1}{4}$,进一步利用(1)中的拆分计算得出答案即可;
(4)由非负数的性质得出a、b的数值,进一步代入计算拆分得出答案即可.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2006}$-$\frac{1}{2007}$
=1-$\frac{1}{2007}$
=$\frac{2006}{2007}$;
(3)原式=$\frac{1}{4}$×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{1003}$-$\frac{1}{1004}$)
=$\frac{1}{4}$×(1-$\frac{1}{1004}$)
=$\frac{1}{4}$×$\frac{1003}{1004}$
=$\frac{1003}{4016}$;
(4)∵|ab-3|与|b-1|互为相反数,
∴|ab-3|+|b-1|=0,
解得:a=3,b=1,
∴原式=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$+…+$\frac{1}{2007×2009}$
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{9}$+…+$\frac{1}{2007}$-$\frac{1}{2009}$)
=$\frac{1}{2}$×(1-$\frac{1}{2009}$)
=$\frac{1}{2}$×$\frac{2008}{2009}$
=$\frac{1004}{2009}$.
故答案为:$\frac{1}{n}$-$\frac{1}{n+1}$;$\frac{2006}{2007}$;$\frac{1003}{4016}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,掌握分数拆分的规律与方法解决问题.


科目:初中数学 来源: 题型:选择题
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
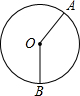 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )| A. | 40°和50° | B. | 80°和100° | C. | 120°和150° | D. | 160°和200° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
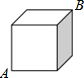 如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )
如图,已知正方体的棱长为1,则蚂蚁在表面上从一个顶点A爬行到相对顶点B的最短路程为( )| A. | 3 | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com