
【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

【答案】(1)①证明见解析;②证明见解析;(2)四边形PEFD是菱形.理由见解析.
【解析】试题分析:(1)①作PM⊥DG于M,根据等腰三角形的性质由PD=PG得MG=MD,根据矩形的判定易得四边形PCDM为矩形,则PC=MD,于是有DG=2PC;
②根据四边形ABCD为正方形得AD=AB,由四边形ABPM为矩形得AB=PM,则AD=PM,再利用等角的余角相等得到∠GDH=∠MPG,于是可根据“ASA”证明△ADF≌△MPG,得到DF=PG,加上PD=PG,得到DF=PD,然后利用旋转的性质得∠EPG=90°,PE=PG,所以PE=PD=DF,再利用DF⊥PG得到DF∥PE,于是可判断四边形PEFD为平行四边形,加上DF=PD,则可判断四边形PEFD为菱形;
(2)与(1)中②的证明方法一样可得到四边形PEFD为菱形.
试题解析:(1)①作PM⊥DG于M,如图1,

∵PD=PG,
∴MG=MD,
∵四边形ABCD为矩形,
∴PCDM为矩形,
∴PC=MD,
∴DG=2PC;
②∵四边形ABCD为正方形,
∴AD=AB,
∵四边形ABPM为矩形,
∴AB=PM,
∴AD=PM,
∵DF⊥PG,
∴∠DHG=90°,
∴∠GDH+∠DGH=90°,
∵∠MGP+∠MPG=90°,
∴∠GDH=∠MPG,
在△ADF和△MPG中, 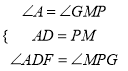 ,
,
∴△ADF≌△MPG(ASA),
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF,
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形;
(2)解:四边形PEFD是菱形.理由如下:
作PM⊥DG于M,如图2,

与(1)一样同理可证得△ADF≌△MPG,
∴DF=PG,
而PD=PG,
∴DF=PD,
∵线段PG绕点P逆时针旋转90°得到线段PE,
∴∠EPG=90°,PE=PG,
∴PE=PD=DF
而DF⊥PG,
∴DF∥PE,
即DF∥PE,且DF=PE,
∴四边形PEFD为平行四边形,
∵DF=PD,
∴四边形PEFD为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了提高学生的身体素质,并争取在学校的体育节中获得好成绩,班级准备从体育用品商店购买跳绳和毽子.已知购买5个毽子和3根跳绳共需85元,购买4个毽子和5根跳绳共需120元.
(1)求一个毽子和一根跳绳各需多少元?
(2)由于购买量大,商店给出如下优惠:毽子6个一盒,整盒出售,每盒27元,跳绳八折优惠.已知班级需要购买的毽子数比跳绳数的2倍多10,总费用不超过395元.问班级最多能购买多少根跳绳?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解:
都可以进行这样的分解:![]() (
(![]() 是正整数,且
是正整数,且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解,并规定
的最佳分解,并规定![]() .
.
例如:18可以分解成![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 是18的最佳分解,所以
是18的最佳分解,所以![]() .
.
(1)如果一个正整数![]() 是另外一个正整数
是另外一个正整数![]() 的平方,我们称正整数
的平方,我们称正整数![]() 是完全平方数.
是完全平方数.
求证:对任意一个完全平方数![]() ,总有
,总有![]() ;
;
(2)如果一个两位正整数![]() ,
,![]() (
(![]() ,
,![]() 为自然数),交换其个位上的数与十位上的数,得到的新数减去原来的两位正整数所得的差为9,那么我们称这个
为自然数),交换其个位上的数与十位上的数,得到的新数减去原来的两位正整数所得的差为9,那么我们称这个![]() 为“求真抱朴数”,求所有的“求真抱朴数”;
为“求真抱朴数”,求所有的“求真抱朴数”;
(3)在(2)所得的“求真抱朴数”中,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数的解析式和一次函数的解析式;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)观察图象直接写出![]() 时
时![]() 的取值范围是 ;
的取值范围是 ;
(4)直接写出:![]() 为
为![]() 轴上一动点,当三角形
轴上一动点,当三角形![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标 .
的坐标 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→)(0,1)→(0,2)→……,且每秒移动一个单位,那么第2018秒时,点所在位置的坐标是( ).

A. (6,44)B. (38,44)C. (44,38)D. (44,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形, ![]() ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想.(不必证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com