
【题目】如图1,![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() ,连结
,连结![]() .
.
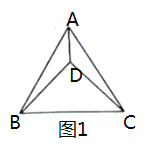
(1)求![]() 的度数
的度数
(2)如图2,以![]() 为斜边在
为斜边在![]() 外作等腰直角
外作等腰直角![]() ,连结
,连结![]()
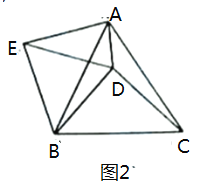
①请判断![]() 的形状,并说明理由
的形状,并说明理由
②若![]() ,求点
,求点![]() 到
到![]() 的距离
的距离
【答案】(1)30° (2)①见详解 ②![]() 到
到![]() 的距离为
的距离为![]()
【解析】
( 1)依据题意先求出△ABD≌△ACD,得出∠BAD=∠CAD,即可求出;
(2)①求出△BCD≌△BAE(ASA),得到△BDE为等边三角形,求出∠AED的度数,即可判断出三角形的形状.
②延长AD与BC交于F点,过E点作EG⊥AD于G,由题意求出ED的值,再通过AF是等边三角形ABC的高,求出GD的值,利用勾股定理求出EG即可.
解:( 1)∵△ABC为等边三角形
∴AB=AC ∠BAC=60°
∵DB=DC AD为△ABD和△ACD公共边
∴ △ABD≌△ACD(SSS)
∴∠BAD=∠CAD=![]() ∠BAC=30°
∠BAC=30°
(2)①∵△BDC和△ABE都是等腰直角三角形
∴![]() ,
,![]()
∵AB=AC
∴△BCD≌△BAE(ASA)
∴EB=BD
∵![]()
∴△BDE为等边三角形
∴EB=ED=EA
∴△ADE为等腰三角形
②如图
延长AD与BC交于F点,过E点作EG⊥AD于G
∵∠BAD=∠CAD
∴AD为∠BAC的角平分线,AF时期延长线
∴AF是∠BAC的角平分线
∵△ABC是等边三角形,三线合一
∴AF⊥BC
∵AB=AC=4 ,∠BAD=30°, △BCD为等腰直角三角形
∴AF=![]() ,DF=2,BD=ED=
,DF=2,BD=ED=![]()
∴AD=![]() -2
-2
∵△ADE为等腰三角形,EG⊥AD
∴AG=GD=![]() AD=
AD=![]()
根据勾股定理得:![]()
![]() =
=![]()
![]() 到
到![]() 的距离
的距离
故答案为:(1)30° (2)①见详解 ②![]() 到
到![]() 的距离为
的距离为![]()


科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾.若租用甲、乙两车运送,两车各运6趟可完成,需支付运费1800元.已知甲、乙两车单独运完此堆垃圾,乙车所运的趟数是甲车的1.5倍,且乙车每趟运费比甲车少100元.
(1)求甲、乙两车单独运完此堆垃圾各需多少趟?
(2)若单独租用一台车,租用哪台车更合算,请你通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量建筑物AB的高度,在D处树立标杆CD,标杆的高是2m,在DB上选取观测点E、F,从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°.从F测得C、A的仰角分别为22°、70°.求建筑物AB的高度(精确到0.1m).(参考数据:tan22°≈0.40,tan58°≈1.60,tan70°≈2.75.)

查看答案和解析>>
科目:初中数学 来源: 题型:
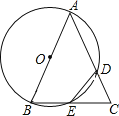
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A、∠B 、∠C、 ∠D 的角平分线恰相交于一点P,记作△APD、△APB、△BPC、△DPC的面积分别为![]() 、
、![]() 、
、![]() 、
、![]() 则下列关系式正确的是( )
则下列关系式正确的是( )
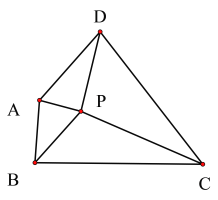
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
![]() 在一个不透明的口袋中有
在一个不透明的口袋中有![]() 个红球和若干个白球,这些球除颜色不同外其他都相同,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下颜色,再把它放回袋中,不断重复上述过程,实验总共摸了
个红球和若干个白球,这些球除颜色不同外其他都相同,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下颜色,再把它放回袋中,不断重复上述过程,实验总共摸了![]() 次,其中有
次,其中有![]() 次摸到了红球,那么估计口袋中有白球多少个?
次摸到了红球,那么估计口袋中有白球多少个?
![]() 请思考并作答:
请思考并作答:
在一个不透明的口袋里装有若干个形状、大小完全相同的白球,在不允许将球倒出来的情况下,如何估计白球的个数(可以借助其它工具及用品)?写出解决问题的主要步骤及估算方法,并求出结果(其中所需数量用![]() 、
、![]() 、
、![]() 等字母表示).
等字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
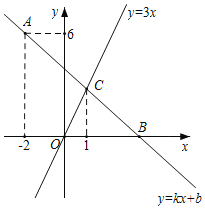
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,6),且与x轴相交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴上,且满足S△COD=S△BOC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com