
【题目】小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):
+5,﹣3,+10,﹣8,﹣6,+12,﹣10.
问:
(1)请说明小虫最后的具体位置?
(2)小虫离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1cm奖励三粒芝麻,则小虫共可得到多少粒芝麻?
【答案】(1)小虫最后的具体位置为出发点O;(2)小虫离开出发点的O最远为12cm;(3)小虫共可得到162粒芝麻.
【解析】
(1)将小虫爬过的路程相加即可得;
(2)从第一个数开始,依次计算每次爬行后离出发点O的位置,再比较各数绝对值的大小即可得;
(3)将小虫爬过的每个路程取绝对值求和得到总的爬行距离,再乘以3即可得.
(1)![]()
则小虫最后的具体位置为出发点O;
(2)小虫每次爬行后,离出发点O的距离如下(正数表示在出发点O的右边、负数表示在出发点O的左边):
第一次爬行后:5
第二次爬行后:![]()
第三次爬行后:![]()
第四次爬行后:![]()
第五次爬行后:![]()
第六次爬行后:![]()
第七次爬行后:![]()
由此可知,小虫离开出发点O的距离分别为5,2,12,4,2,10,0
故小虫离开出发点O最远距离为12厘米;
(3)总的爬行距离为![]()
![]()
![]()
则可得到的芝麻粒数为![]() (粒)
(粒)
故小虫共可得到162粒芝麻.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
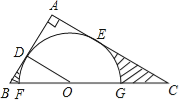
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A和B在数轴上对应的数分别为a和b,且(a+5)2+|b﹣4|=0.
(1)求线段AB的长;
(2)点C在数轴上所对应的数为x,且x是方程x﹣3=![]() x﹣1的解,在线段BC上是否存在点D,使得AD+BD=
x﹣1的解,在线段BC上是否存在点D,使得AD+BD=![]() CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
(3)如图,PO=1,点P在AB的上方,且∠POB=60°,点P绕着点O以30度/秒的速度在圆周上顺时针旋转一周停止,同时点Q沿线段AB自点A向点B运动,若P、Q两点能相遇,求点Q的运动速度.
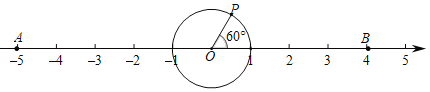
查看答案和解析>>
科目:初中数学 来源: 题型:
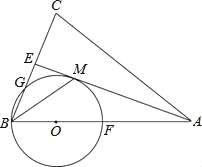
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
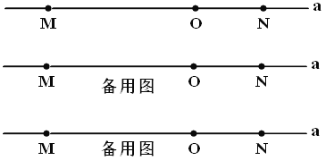
【题目】如图,直线![]() 上有
上有![]() 、
、![]() 两点,
两点,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() .
.
(1)填空:![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(2)若点![]() 是线段
是线段![]() 上一点,且满足
上一点,且满足![]() ,求
,求![]() 的长;
的长;
(3)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,向右运动,点
两点同时出发,向右运动,点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .设运动时间为
.设运动时间为![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 、
、![]() 两点停止运动.
两点停止运动.
①当![]() 为何值时,
为何值时,![]() ?
?
②当点![]() 经过点
经过点![]() 时,动点
时,动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度也向右运动,当点
的速度也向右运动,当点![]() 追上点
追上点![]() 后立即返回,以
后立即返回,以![]() 的速度向点
的速度向点![]() 运动,遇到点
运动,遇到点![]() 后再立即返回,以
后再立即返回,以![]() 的速度向点
的速度向点![]() 运动,如此往返,直到点
运动,如此往返,直到点![]() 、
、![]() 停止运动时,点
停止运动时,点![]() 也停止运动.求出在此过程中点
也停止运动.求出在此过程中点![]() 运动的总路程是多少?
运动的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生初中毕业体育考试的成绩统计如下表:
成绩(分) | 35 | 39 | 42 | 44 | 45 | 48 | 50 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的平均数是45
C.该班学生这次考试成绩的中位数是45
D.该班学生这次考试成绩的众数是45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,每个自然数都有因数,对于一个自然数![]() ,我们把小于
,我们把小于![]() 的正的因数叫做
的正的因数叫做![]() 的真因数.如10的正因数有1、2、5、10,其中1、2、5是10的真因数.把一个自然数
的真因数.如10的正因数有1、2、5、10,其中1、2、5是10的真因数.把一个自然数![]() 的所有真因数的和除以
的所有真因数的和除以![]() ,所得的商叫做
,所得的商叫做![]() 的“完美指标”.如10的“完美指标”是
的“完美指标”.如10的“完美指标”是![]() .一个自然数的“完美指标”越接近1,我们就说这个数越“完美”.如8的“完美指标”是
.一个自然数的“完美指标”越接近1,我们就说这个数越“完美”.如8的“完美指标”是![]() ,10的“完美指标”是
,10的“完美指标”是![]() ,因为
,因为![]() 比5更接近1,所以我们说8比10更完美.
比5更接近1,所以我们说8比10更完美.
(1)试计算5的“完美指标”.
(2)试计算6和9的“完美指标”.
(3)试找出15到20的自然数中,最“完美”的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象经过点A,且点A到x轴的距离是4.
的图象经过点A,且点A到x轴的距离是4.
(1) 求点A的坐标;
(2) 点![]() 为坐标原点,点
为坐标原点,点![]() 是x轴正半轴上一点,当
是x轴正半轴上一点,当![]() 时,求直线AB的解析式.
时,求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年春节是市民购买葡萄酒的高峰期,某商场分两批购进同一种葡萄酒,第一批所用资金是8000元,第二批所用资金是10000元.第二批葡萄酒每瓶比第一批葡萄酒每瓶贵90元,结果购买数量比第一批少20%.
(1)求该商场两次共购进多少瓶葡萄酒.
(2)第一批葡萄酒的售价是每瓶200元,很快售完,但因为进价的提高第二批葡萄酒的售价在第一批基础上提高了2a%,实际售卖对比第一批少卖a%,结果两次销售共赚得利润3200元,求a(其中a>25).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com