
 如图,AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连结
如图,AB是⊙O的直径,PA是⊙O的切线,过点B作BC∥OP交⊙O于点C,连结| 2 |
| 2 |
| 1 |
| 2 |
| PA2+OA2 |
| 3 |
| BC |
| OA |
| AB |
| OP |
| AB•OA |
| OP |
| 2×1 | ||
|
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
| A、(x-1)2=7 |
| B、(x+1)2=7 |
| C、(x-1)2=6 |
| D、(x+1)2=12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 用小立方块搭一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;
用小立方块搭一个几何体,使它的从正面和从上面看到的这个几何体的形状图如图所示,从上面看到的形状图中的小正方形中的字母表示该位置小立方块的个数,试回答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:
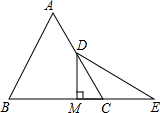 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com