

分析 (1)由等腰直角三角形的性质得到AP=BP=$\frac{\sqrt{2}}{2}$AB,根据三角形中位线的性质,得到EF∥AB,EF=$\frac{1}{2}$AB,再由勾股定理得到结果;
(2)连接EF,由AE2=PE2+PA2,AC2=(2AE)2=4AE2同理BC2=(2BF2)类比着(1)即可证得结论.
(3)连接AC交EF于H,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,根据E,F分别是AD,BC的中点,得到AE=BF=CF=$\frac{1}{2}$AD,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由(2)的结论得即可得到结果.
解答 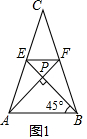 解:(1)如图1,∵AF⊥BE,∠ABE=45°,
解:(1)如图1,∵AF⊥BE,∠ABE=45°,
∴AP=BP=$\frac{\sqrt{2}}{2}$AB=2,
∵AF,BE是△ABC的中线,
∴EF∥AB,EF=$\frac{1}{2}$AB=$\sqrt{2}$,
∴∠PFE=∠PEF=45°,
∴PE=PF=1,
在Rt△FPB和Rt△PEA中,
AE=BF=$\sqrt{5}$,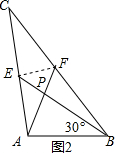
∴AC=BC=2$\sqrt{5}$,
∴a=b=2$\sqrt{5}$,
如图2,连接EF,
同理可得:EF=$\frac{1}{2}$×4=2,
∵EF∥AB,
∴△PEF~△ABP,
∴$\frac{PF}{AP}$=$\frac{PE}{PB}$=$\frac{EF}{AB}$=$\frac{1}{2}$,
在Rt△ABP中,
AB=4,∠ABP=30°,
∴AP=2,PB=2$\sqrt{3}$,
∴PF=1,PE=$\sqrt{3}$,
在Rt△APE和Rt△BPF中,
AE=$\sqrt{7}$,BF=$\sqrt{13}$,
∴a=2$\sqrt{13}$,b=2$\sqrt{7}$,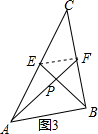
故答案为:2$\sqrt{5}$,2$\sqrt{5}$,2$\sqrt{13}$,2$\sqrt{7}$;
(2)猜想:a2+b2=5c2
证明:如图3,设PE=m,PF=n,那么PB=2m,PA=2n.
根据勾股定理得:∵AE2=PE2+PA2=m2+(2n)2=m2+4n2
∴AC2=(2AE)2=4AE2=4(m2+4n2)=4m2+16n2=b2
同理BC2=(2BF2)=4BF2=4(n2+4m2)=4n2+16m2=a2
∴a2+b2=(4n2+16m2)+(4m2+16n2)=20m2+20n2=5(4m2+4n2)
又∵AB2=PA2+PB2=(2n)2+(2m)2=4m2+4n2=c2
∴a2+b2=5c2;
(3)如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,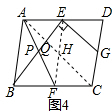
∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=2$\sqrt{17}$,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴AE=$\frac{1}{2}$AD,BF=$\frac{1}{2}$BC,
∴AE=BF=CF=$\frac{1}{2}$AD=$\sqrt{17}$,
∵AE∥BF,
∴四边形ABFE是平行四边形,
∴EF=AB=6,AP=PF,
在△AEH和△CFH中,
$\left\{\begin{array}{l}{∠EAH=∠FCH}\\{∠AHE=∠FHC}\\{AE=CF}\end{array}\right.$,
∴△AEH≌△CFH(AAS),
∴EH=FH,
∴EQ,AH分别是△AFE的中线,
由(2)的结论得:AF2+EF2=5AE2,
∴AF2=5($\sqrt{17}$)2-EF2=49,
∴AF=7.
点评 本题考查了相似三角形的判定和性质、勾股定理、全等三角形的判定与性质等知识,注意类比思想在本题中的应用,得出AF2+EF2=5AE2是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
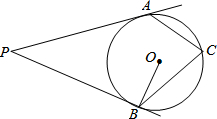 如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )
如果,过圆O外一点P引圆O的切线PA,PB,切点为A,B,C为圆上一点,若∠APB=50°,则∠ACB=( )| A. | 50° | B. | 60° | C. | 65° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com