
【题目】如图,⊙O 的内接四边形 ABCD 两组对边延长线分别交于点 E、F.
(1)若∠E=∠F,求证:∠ADC=∠ABC;
(2)若∠E=∠F=40°,求∠A 的度数;
(3)若∠E=30°,∠F=40°,求∠A 的度数.

【答案】(1)见解析;(2)50°;(3)55°.
【解析】
(1)根据外角的性质即可得到结论;
(2)根据圆内接四边形的性质和等量代换即可求得结果;
(3)连结EF,如图,根据圆内接四边形的性质得∠ECD=∠A,再根据三角形外角性质得∠ECD=∠1+∠2,则∠A=∠1+∠2,然后根据三角形内角和定理有∠A+∠1+∠2+∠E+∠F=180°,解方程即可.
(1)∠E=∠F,
∵∠DCE=∠BCF,
∠ADC=∠E+∠DCE,∠ABC=∠F+∠BCF,
∴∠ADC=∠ABC;
(2)由(1)知∠ADC=∠ABC,
∵∠EDC=∠ABC,
∴∠EDC=∠ADC,
∴∠ADC=90°,
∴∠A=90°﹣40°=50°;
(3)连结 EF,如图,
∵四边形 ABCD 为圆的内接四边形,
∴∠ECD=∠A,
∵∠ECD=∠1+∠2,
∴∠A=∠1+∠2,
∵∠A+∠1+∠2+∠E+∠F=180°,
∴2∠A+30°+40°=180°,
∴∠A =55°.


科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )

A. 22cmB. 20cmC. 18cmD. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择
单车”已成为很多市民出行的选择![]() 张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为
张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为![]() 单位:千米
单位:千米![]() ,乘坐地铁的时间为
,乘坐地铁的时间为![]() 单位分钟
单位分钟![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根据表中数据的规律,直接写出表格中a、b的值和
根据表中数据的规律,直接写出表格中a、b的值和![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 张老师骑单车的时间
张老师骑单车的时间![]() 单位:分钟
单位:分钟![]() 也受x的影响,其关系可以用
也受x的影响,其关系可以用![]() 米描述,
米描述,
![]() 若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
![]() 若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
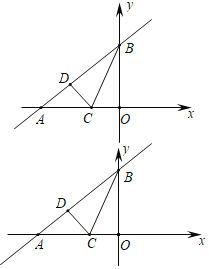
【题目】已知:直线y=![]() x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
将△CBO沿BC折叠后,点O恰好落在AB边上点D处
(1)求直线BC的解析式;
(2)求点D的坐标;
(3)P为平面内一动点,且以A、B、C、P为顶点的四边形为平行四边形,直接写出点P坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题
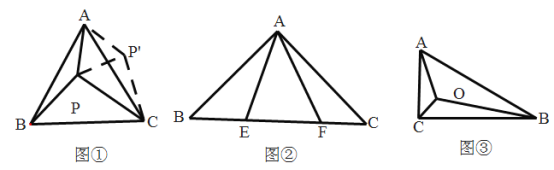
(1)阅读理解:如图①,等边![]() 内有一点
内有一点![]() ,若点
,若点![]() 到顶点
到顶点![]() ,
,![]() ,
,![]() 的距离分别为3,4,5,求
的距离分别为3,4,5,求![]() 的大小.
的大小.
思路点拨:考虑到![]() ,
,![]() ,
,![]() 不在一个三角形中,采用转化与化归的数学思想,可以将
不在一个三角形中,采用转化与化归的数学思想,可以将![]() 绕顶点
绕顶点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() 处,此时
处,此时![]() ,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出
,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出![]() 的度数.请你写出完整的解题过程.
的度数.请你写出完整的解题过程.
(2)变式拓展:请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为
为![]() 上的点且
上的点且![]() ,
,![]() ,
,![]() ,求
,求![]() 的大小.
的大小.
(3)能力提升:如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值,即
的值,即![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com