Question

【题目】已知，在△ABC中，AB=AC．过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ，直线a交BC边于点P（点P不与点B、点C重合），△BMN的边MN始终在直线a上（点M在点N的上方），且BM=BN，连接CN．

（1）当∠BAC=∠MBN=90°时，

①如图a，当θ=45°时，∠ANC的度数为　 　；

②如图b，当θ≠45°时，①中的结论是否发生变化？说明理由；

（2）如图c，当∠BAC=∠MBN≠90°时，请直接写出∠ANC与∠BAC之间的数量关系，不必证明．

Answer 1

【答案】（1）①45°；②当θ≠45°时，①中的结论不发生变化，理由见解析；（2）∠ANC=90°﹣∠BAC．

【解析】试题分析：（1）①证明四边形ABNC是正方形，根据正方形的对角线平分一组对角线即可求解；

②根据等腰直角三角形的性质可得∠BNP=∠ACB，然后证明△BNP和△ACP相似，根据相似三角形对应边成比例可得，再根据两边对应成比例夹角相等可得△ABP和△CNP相似，然后根据相似三角形对应角相等可得∠ANC=∠ABC，从而得解；

（2）根据等腰三角形的两底角相等求出∠BNP=∠ACB，然后证明△BNP和△ACP相似，根据相似三角形对应边成比例可得，再根据两边对应成比例夹角相等可得△ABP和△CNP相似，然后根据相似三角形对应角相等可得∠ANC=∠ABC，然后根据三角形的内角和定理列式整理即可得解．

试题解析：（1）①∵∠BAC=90°，θ=45°，∴AP⊥BC，BP=CP（等腰三角形三线合一），

∴AP=BP（直角三角形斜边上的中线等于斜边的一半），

又∵∠MBN=90°，BM=BN，∴AP=PN（等腰三角形三线合一），

∴AP=PN=BP=PC，且AN⊥BC，∴四边形ABNC是正方形，∴∠ANC=45°；

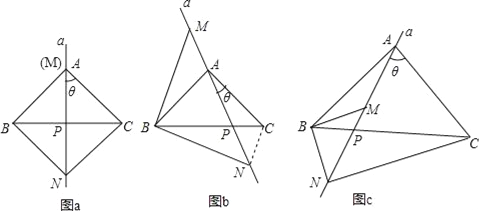
②连接CN，当θ≠45°时，①中的结论不发生变化．

理由如下：∵∠BAC=∠MBN=90°，AB=AC，BM=BN，∴∠ABC=∠ACB=∠BNP=45°，

又∵∠BPN=∠APC，∴△BNP∽△ACP，∴，

又∵∠APB=∠CPN，∴△ABP∽△CNP，

∴∠ANC=∠ABC=45°；

（2）∠ANC=90°﹣∠BAC．

理由如下：∵∠BAC=∠MBN≠90°，AB=AC，BM=BN，

∴∠ABC=∠ACB=∠BNP=（180°﹣∠BAC），

又∵∠BPN=∠APC，∴△BNP∽△ACP，∴，

又∵∠APB=∠CPN，∴△ABP∽△CNP，∴∠ANC=∠ABC，

在△ABC中，∠ABC=（180°﹣∠BAC）=90°﹣∠BAC．