
【题目】如图,在平面直角坐标系xOy中,二次函数![]() 的图象与y轴交于C点,与x轴交于A、B两点(A点在B点右侧),一次函数
的图象与y轴交于C点,与x轴交于A、B两点(A点在B点右侧),一次函数![]() 的图象经过A、C两点,已知
的图象经过A、C两点,已知![]() .
.
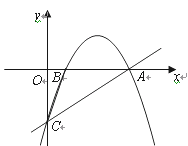
(1)求该二次函数和一次函数的解析式
(2)连接BC,求△ABC的面积
【答案】(1) ![]() ; (2)3.
; (2)3.
【解析】
(1)由二次函数y=![]() x2+bx2的解析式可求出和y轴交点的坐标即点C的坐标,由已知条件求出OA的长度进而求出点A的坐标,把A,C的坐标分别代入即可求出二次函数和一次函数的解析式;
x2+bx2的解析式可求出和y轴交点的坐标即点C的坐标,由已知条件求出OA的长度进而求出点A的坐标,把A,C的坐标分别代入即可求出二次函数和一次函数的解析式;
(2)令y=0,求出B点的坐标即OB的长度,所以AB的长度可以求出,又因为AB上的高为OC,利用面积公式即可求出△ABC的面积.
(1)在y=![]() x2+bx2中,
x2+bx2中,
令x=0,得y=-2,
∴C(0,-2),
∴OC=2,
在Rt△AOC中,OA=![]() =4,
=4,
∴A(4,0).
∵y=![]() x2+bx2过A(4,0),
x2+bx2过A(4,0),
∴0=![]() ×42+b×42,
×42+b×42,
∴b=![]() ,
,
∴y=![]() x2+
x2+![]() x2.
x2.
∵y=mx+n(m≠0)过A(4,0)、C(0,-2),
∴![]() ,
,
∴ ,
,
∴y=![]() x-2;
x-2;
(2)在y=![]() x2+
x2+![]() x2中,
x2中,
令y=0,得x1=1,x2=4,
∴B(1,0),
∴OB=1,
∴AB=OA-OB=3,
∴S△ABC=![]() ×ABOC=
×ABOC=![]() ×3×2=3.
×3×2=3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…第n次移动到An.则△OA6A2020的面积是( )
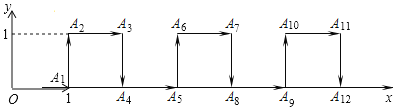
A.505![]() B.504.5
B.504.5![]() C.505.5
C.505.5![]() D.1010
D.1010![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(3,a)(其中a>4),射线OA与反比例函数y=![]() 的图象交于点P,点B、C分别在函数y=
的图象交于点P,点B、C分别在函数y=![]() 的图象上,且AB∥x轴,AC∥y轴;
的图象上,且AB∥x轴,AC∥y轴;
(1)当点P横坐标为2,求直线AO的表达式;
(2)连接CO,当AC=CO时,求点A坐标;
(3)连接BP、CP,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查甲,乙两台包装机分装标准质量为![]() 奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:![]() )如下:
)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量( | 甲 | 乙 |
| ____________ | 0 |
| 0 | 3 |
| 3 | 1 |
| 0 | ____________ |
| ____________ | 1 |
| 3 | 0 |
分析数据:
表二
种类 | 甲 | 乙 |
平均数 | 401.5 | 400.8 |
中位数 | ____________ | 402 |
众数 | 400 | ____________ |
方差 | 36.85 | 8.56 |
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则![]() 的值为 .
的值为 .
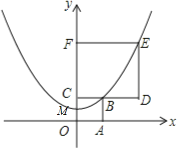
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
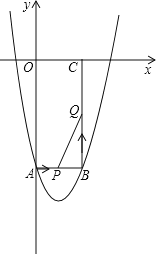
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
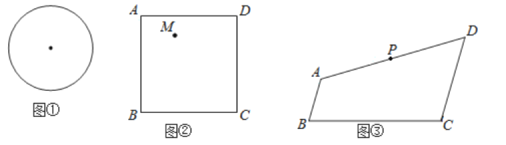
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,![]() 是正方形
是正方形![]() 内一定点,请在图②中作出两条直线(要求其中一条直线必须过点
内一定点,请在图②中作出两条直线(要求其中一条直线必须过点![]() ),使它们将正方形
),使它们将正方形![]() 的面积四等分:
的面积四等分:
问题解决
(3)如图③,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点如果
的中点如果![]() ,且
,且![]() ,那么在边
,那么在边![]() 上足否存在一点
上足否存在一点![]() ,使
,使![]() 所在直线将四边形
所在直线将四边形![]() 的面积分成相等的两部分?若存在,求出
的面积分成相等的两部分?若存在,求出![]() 的长:若不存在,说明理由.
的长:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合探究:观察发现:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
…
建立模型:形如![]() 的化简(其中
的化简(其中![]() ,
,![]() 为正整数),只要我们找到两个正整数
为正整数),只要我们找到两个正整数![]() ,
,![]() (
(![]() ),使
),使![]() ,
,![]() ,那么
,那么![]() .问题解决:
.问题解决:
(1)根据观察证明“建立模型”的结论是正确的;
(2)化简:①![]() ;
;
②![]() ;
;
(3)已知一个长方形的长为![]() ,宽为
,宽为![]() ,若某正方形的面积与该长方形的面积相等,设正方形边长为
,若某正方形的面积与该长方形的面积相等,设正方形边长为![]() ,求正方形的边长.
,求正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校500名毕业生中考体育加试测试情况进行调查,根据男生1 000m及女生800m测试成绩整理、绘制成如下不完整的统计图(图①、图②),请根据统计图提供的信息,回答下列问题:
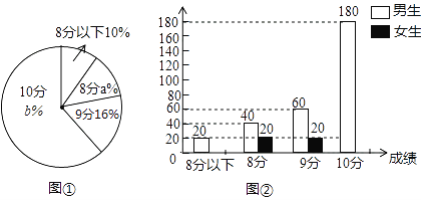
(1)该校毕业生中男生有________人,女生有________人;
(2)扇形统计图中a=________,b=________;
(3)补全条形统计图(不必写出计算过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com