
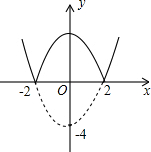
 如图,将二次函数y=x2-4位于x的下方的图象沿x轴翻折,得到一个新函数的图象(图中的实线)
如图,将二次函数y=x2-4位于x的下方的图象沿x轴翻折,得到一个新函数的图象(图中的实线)
| a |
| 2 |


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
 观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )
观察如图所摆放的五朵梅花,平移中间的一朵梅花,下列说法错误的是( )| A、沿对角线平移到左上角即可得到左上角梅花 |
| B、沿对角线平移到右上角,再顺时针旋转90°可得到右上角梅花 |
| C、沿对角线平移到右下角,再旋转180°可得到右下角梅花 |
| D、沿对角线平移到左下角,再顺时针旋转90°可得到左下角梅花 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
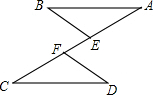 如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是
如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com