
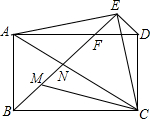
 如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9.
如图,矩形ABCD中,AB=3,AD=4,△ACE为等腰直角三角形,∠AEC=90°,连接BE交AD、AC分别于F、N,CM平分∠ACB交BN于M,则MN:NF=5:9. 分析 根据勾股定理求得AC=5,由∠ABC=∠AEC=∠ADC=90°,根据圆周角定理的推论得到点A、B、C、D、E都在以AC为直径的圆上,再根据圆周角定理得到∠AEB=∠ACB,∠DAC=∠CED,∠EAD=∠ECD,易证△AEF≌△CED,即可得到AB=AF=3,根据勾股定理得出BF=3$\sqrt{2}$;根据全等三角形的性质得出∠ABF=∠AFB=45°,再利用等腰直角三角形可得AE=ME=$\frac{5\sqrt{2}}{2}$,再证得△EFD是等腰直角三角形求得EF=$\frac{\sqrt{2}}{2}$,从而求得BM,由AF∥BC,得到NB=$\frac{4}{7}$BF,FN=$\frac{3}{7}$BF,即可求得MN,从而求得结果.
解答 解:在RT△ABC中,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵△ACE为等腰直角三角形,
∴AE=CE=$\frac{\sqrt{2}}{2}$AC=$\frac{5\sqrt{2}}{2}$,
∵∠ABC=∠AEC=∠ADC=90°,
∴点A、B、C、D、E都在以AC为直径的圆上,
∴∠AEB=∠ACB,∠DAC=∠CED,∠EAD=∠ECD,
而∠DAC=∠ACB,
∴∠AEB=∠CED,
在△AEF和△CED中
$\left\{\begin{array}{l}{∠AEB=∠CED}\\{AE=CE}\\{∠EAD=∠ECD}\end{array}\right.$
∴△AEF≌△CED(ASA),
∴AF=CD,
而CD=AB,
∴AB=AF=3,
∴DF=4-3=1,
∵∠BAF=90°,
∴BF=3$\sqrt{2}$,
∴∠ABF=∠AFB=45°,
∴∠EMC=∠MCB+45°,
而∠ECM=∠NCM+45°,
∵CM平分∠ACB交BN于M,
∴∠EMC=∠ECM,
∴EC=EM=$\frac{5\sqrt{2}}{2}$,
∵AF∥BC,AF=3,BC=4,
∴$\frac{AF}{BC}$=$\frac{NF}{BN}$=$\frac{3}{4}$,
∵BF=3$\sqrt{2}$,
∴NF=$\frac{3}{7}$BF=$\frac{3}{7}$×3$\sqrt{2}$=$\frac{9}{7}$$\sqrt{2}$,
BN=$\frac{4}{7}$BF=$\frac{4}{7}$BF=$\frac{12}{7}$$\sqrt{2}$,
∵∠EDA=∠EAC=45°,
而∠EFD=∠AFB=45°,
∴∠FED=90°
∴△EFD是等腰直角三角形,
∴EF=$\frac{\sqrt{2}}{2}$,
∴BE=BF+EF=3$\sqrt{2}$+$\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{2}$,
∴BM=BE-ME=$\frac{7\sqrt{2}}{2}$-$\frac{5\sqrt{2}}{2}$=$\sqrt{2}$,
∴MN=BN-BM=$\frac{12\sqrt{2}}{7}$-$\sqrt{2}$=$\frac{5\sqrt{2}}{7}$,
∴$\frac{MN}{NF}$=$\frac{\frac{5\sqrt{2}}{7}}{\frac{9\sqrt{2}}{7}}$=$\frac{5}{9}$,
即MN:NF=5:9.
故答案为5:9.
点评 本题考查了圆周角定理以及推论:同弧所对的圆周角相等,90度的圆周角所对的弦为直径;也考查了等腰三角形和矩形的性质、勾股定理以及三角形相似的判定与性质.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
 如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.
如图,已知一艘渔船上的渔民在B处看见灯塔M在北偏东27°方向,这艘渔船以28海里/时的速度向正西方向航行,半小时后到达A处,在A处看见灯塔M在北偏东60°方向,请你运用以上测得的数据求出此时灯塔M与渔船的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
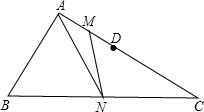 如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.
如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com