
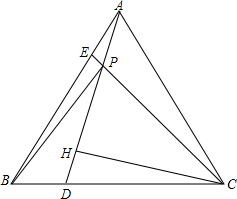
 如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.
如图,△ABC是等边三角形,D、E分别在BC、AB上,且AE=BD,连接AD、CE交于P,过点C作CH⊥AD于H.分析 (1)由等边三角形的三条边相等、三个内角都是60°可以推知:AC=AB,∠ACE=∠ABD=60°,然后结合已知条件,利用全等三角形的判定定理SAS证得结论;
(2)因为CH⊥AD,△PCH为直角三角形,由△ACE≌△BAD得出∠AEP=∠ADB,进一步得出∠APE=∠ABD=60°,则∠CPH=∠APE=60°,进一步求得∠PCH=30°解决问题;
(3)先判断出AH=2AP,进而判断出△ABH≌△CAP,即可得出∠PBH=∠BPH=30°,即可得出结论.
解答 证明:(1)
∵△ABC是等边三角形,
∴AC=AB,∠ACE=∠ABD=60°.
在△ACE与△ABD中,$\left\{\begin{array}{l}{AC=AB}\\{∠ACE=∠ABD}\\{AE=BD}\end{array}\right.$,
∴△ACE≌△ABD(SAS);
(2)解:∵CH⊥AD,
∴△PCH为直角三角形,
∵△ACE≌△BAD,
∴∠AEP=∠ADB,
∴∠APE=∠ABD=60°,
∴∠CPH=∠APE=60°,
∴∠PCH=30°,
∴PC=2PH,
即$\frac{PC}{PH}$=2,
(3)BP⊥PC.
理由:如图,连接BH,
∵AH2+AH•AP-6AP2=0,
∴(AH+3AP)(AH-2AP)=0,
∴AH=2AP,
∴AP=PH,
由(2)知,PC=2PH,
∴PC=AH,
在△ABH和△CAP中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠ACP}\\{AH=PC}\end{array}\right.$,
∴△ABH≌△CAP,
∴∠BHP=∠APC=120°,BH=AP,
∵AP=PH,
∴BH=PH,
∴∠PBH=∠BPH,
∴∠BPH=$\frac{180°-∠BHP}{2}$=30°,
∵∠CPH=60°
∴∠BPC=∠BPH+∠HPC=90°,
∴BP⊥PC.
点评 此题是三角形综合题,主要考查等边三角形的性质、三角形全等的判定与性质及有30°角的直角三角形的性质等知识;熟练综合运用基本知识解决问题,得出AH=2AP是解本题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2:3:1 | B. | 5:2:2 | C. | 8:1:19 | D. | 8:1:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC三个顶点的坐标分别为A(-2,5),B(-5,1),C(-2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )
如图,△ABC三个顶点的坐标分别为A(-2,5),B(-5,1),C(-2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )| A. | (1,2) | B. | (2,1) | C. | (1,1) | D. | (2,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com